Um vagonete de mina carregado com peso de 5.000 lb está sendo içado por uma polia sem atrito e um cabo de aço, como mostrado na Figura 2.42. Determine a frequência natural de vibração do vagonete na posição dada.
Passo 1
Bora, galera!
Pra começar vamos ajustar essa questão um pouquinho e passar todos os seus valores para as nossas unidades de medida (que são a mesma do nosso querido SI) para, então, entendermos como iremos resolver.
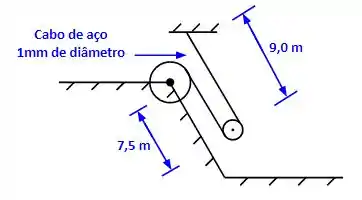
Massa: 2267,7 kg
Módulo de Young do Aço = 200 Gpa
Área =
Prontinho!
Passo 2
Agora, devemos encontrar o valor da constante de mola equivalente para que, então, a gente possa substituir na nossa fórmula de frequência natural.
Para isso, temos que
Passo 3
Como x é medido a partir do comprimento não esticado do cabo a equação de movimento é
,
onde
Assim, a frequência natural do sistema é dada por