Para uma viga em balanço com o carregamento mostrado, determinar a declividade e a deflexão no ponto B. Usar .
- Deflexão do ponto B
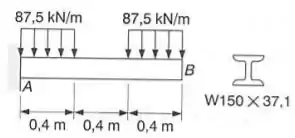
Passo 1
Então galerinha, esse exercício é bem tranquilo, podemos usar o nosso conceito de sobreposição de cargas, aqui podemos notar o seguinte, podemos dividir a carga da seguinte maneira na nossa viga:
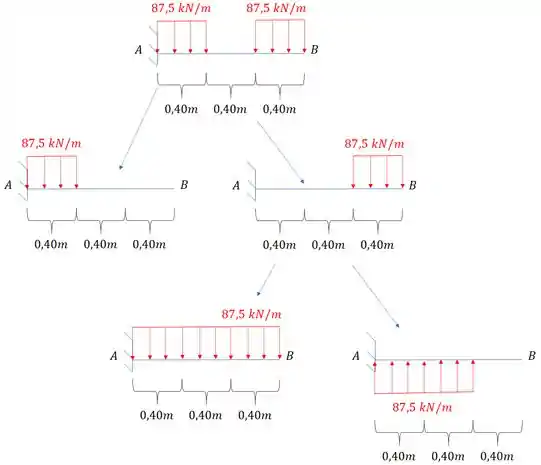
Assim temos 3 vigas a serem analisadas:
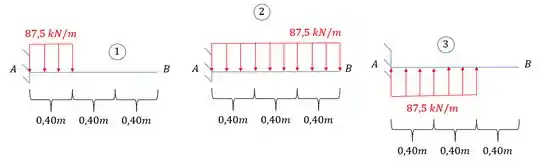
E a tabela que temos no fim do livro é dado por:
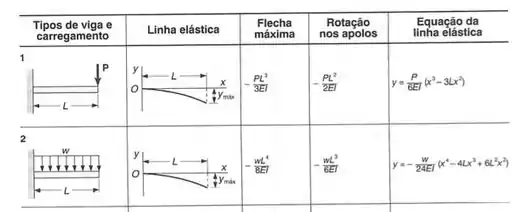
E para a barra com carga distribuída, precisamos ver que não temos a equação exata para o ponto B, mas podemos usar a nossa equação exatamente até o ponto em que a carga distribuída acaba, considerando esse o ponto final em cada barra, e depois, a partir do ponto que termina, podemos chegar na deformação do ponto B, assim, temos que:
Assim temos que:
- Deformação em B na viga 1
- Deformação em B na viga 2
- Deformação em B na viga 3
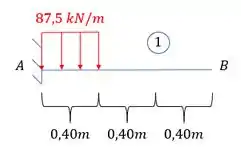
E olhando o ângulo em , teremos que:
E a deformação em D, considerando a distância entre B e D como “b”, teremos que:
Assim tem-se que:
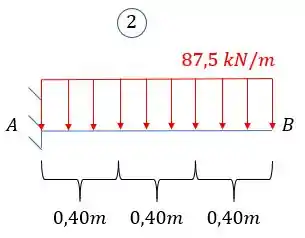
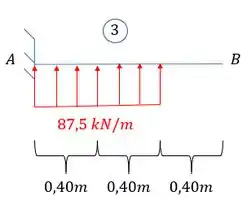
Como a carga é de baixo pra cima, mudamos o sinal, assim temos que:
E olhando o ângulo em , teremos que:
E a deformação em D, considerando a distância entre B e D como “b”, teremos que:
Assim tem-se que:
Passo 2
Para obtermos a deformação final no ponto B, precisamos somar todas as deformações levando em consideração o sinal, assim temos que:
Sabemos que:
Assim a deformação é dada por: