Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 8
resolver as partes e do , considerando que a viga é um perfil laminado de aço e que , e .
Passo 1
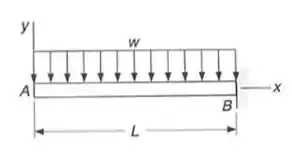
Fala galera, agora vamos aplicar os mesmos conceitos que já vamos aplicar os mesmos princípios que já vimos, mas agora vamos obter a nossa fórmula e os nossos dados levando em consideração a viga que o enunciado está nos dando.
Vamos nos preocupar com a equação em si no próximo passo, vamos agora obter alguns dados importantes para solução do nosso problema.
Sabemos que a nossa equação é dada por:
Já sabemos pelo enunciado que:
Sabemos que é a equação da nossa reta, e essa equação é simplificada da seguinte maneira:
E sabemos que o comprimento da nossa barra é dada por:
E o momento de inércia podemos obter pela seguinte tabela (lembrando que vamos considerar o nosso eixo em pé, ou seja, queremos o momento de inércia em torno de x na nossa tabelinha aqui de baixo.
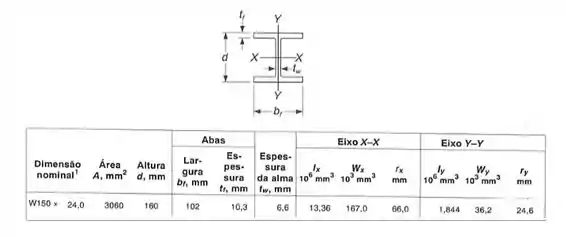
E por fim precisamos pensar o seguinte, se quisermos definir a deformação da extremidade da viga, precisamos usar o valor de:
Porque a extremidade da viga é o oposto ao engaste, e nesse caso, está iniciado no ponto 0. Agora que já temos os dados a serem substituídos, vamos definir a nossa equação e depois só substituirmos.
Passo 2
Vamos, lá, no nosso problema, a estrutura dada é:
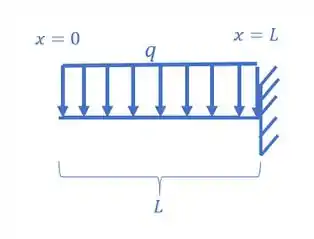
Como a nossa carga é distribuída, independente que essa carga seja no meio, ou no final ou no começo, teremos que:
Substituindo na nossa equação, teremos que:
Se integramos a primeira vez, vamos obter a primeira constante do nosso problema:
E vale lembrar que como já definimos, a primeira integral é o cortante, assim temos que:
Se integrarmos novamente, teremos a nossa segunda incógnita:
E sabemos que esse é o nosso momento fletor:
Se integramos novamente, teremos a nossa terceira incógnita:
E essa é a equação da rotação da nossa viga:
E por fim, a ultima integral vai dar o deslocamento e a nossa quarta incógnita:
Tendo a equação, basta olharmos as condições de contorno, e com elas podemos determinar a solução do nosso problema, vamos nessa? Já está acabando.
Passo 3
Para as condições, iremos olhar os extremos da viga, e é importante ver o seguinte, sempre a soma das condições de contorno deve ser igual ao número de incógnitas, ou seja, se temos 4 incógnitas, temos que ter 4 condições, podendo ser qualquer combinação de essenciais com naturais ( 1 natural e 3 essenciais, ou duas essenciais e duas naturais, ou 4 essenciais) não importa, no fim o total tem que ser 4, sendo assim teremos que:
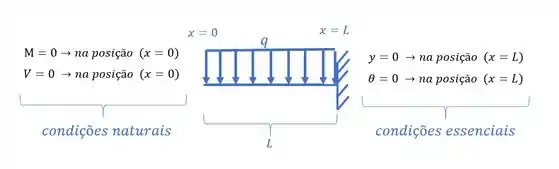
Ou seja, temos 4 condições, e com isso podemos resolver o nosso problema, sempre começando do menor número de incógnitas para o maior, sendo assim vamos ter que:
Definido a primeira incógnita, vamos para a próxima:
Já sabemos quanto vale .
E sabemos que quando
Substituindo temos que:
Substituindo teremos que:
E assim determinamos todas as incógnitas do nosso problema, sendo assim basta substituirmos na nossa equação final.
Passo 4
O item b) quer saber o deslocamento na extremidade da barra, ou seja, que saber o deslocamento em , assim temos que:
Sabemos que:
Substituindo, teremos que:
No item c) queremos saber a rotação, para isso sabemos que a equação é dada por:
Substituindo na posição
Sabemos que:
Substituindo, teremos que:
E assim resolvemos o nosso problema, vamos para o próximo?