Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 61b
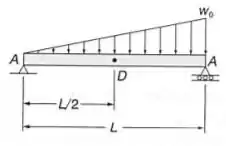
Para a viga com o carregamento mostrado, determinar:
- A localização do ponto que ocorre o máximo para a Viga e carregamento do
Passo 1
Então galera, até aqui vimos casos de vigas simétricas, e esse caso pode acabar nos dando um medinho, mas pode ficar tranquilo, porque todas as premissas continuam iguais, a diferença está em como vamos usar ela, e para isso, sabemos de cara que precisamos das nossas reações de apoio, com isso, temos que:
Agora perceba o seguinte, suponha que ao invés de termos os apoios em A, vamos supor que eles são cargas aplicadas na nossa viga, e que no caso no ponto B temos um engaste, então basta desenharmos o diagrama de cada carga com relação ao ponto B, assim, teremos que:
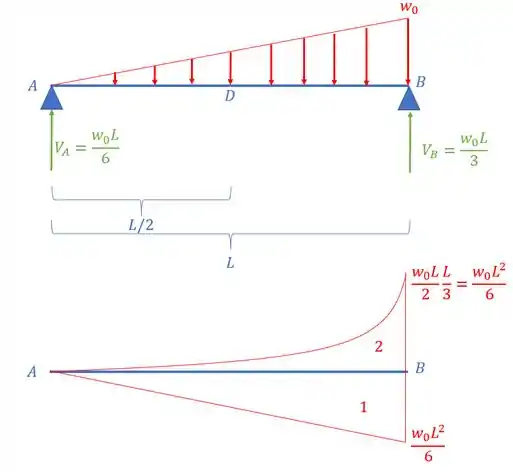
E sabemos que devemos dividir o nosso diagrama por , e assim teremos que:
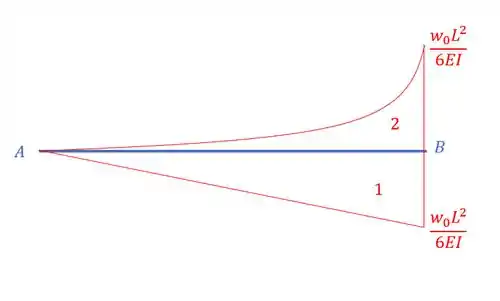
Passo 2
Agora precisamos pensar no seguinte, sabemos que o máximo ponto de deflexão, ocorre onde a inclinação desse ponto é horizontal, ou seja, quando a inclinação é zero, porém, não sabemos onde esse ponto está, por isso, podemos supor então que esse ponto ocorre em um certo local chamado de K, onde nesse ponto K, a inclinação é zero, assim, temos que:
Como estamos usando o ponto A como referência, temos que usar a distância entre o ponto e o ponto A, assim, teremos que:
Sabemos que o ponto que ocorre o máximo é o ponto em que a inclinação é zero, assim sabemos que , assim temos que:
E pelo item A sabemos que:
Assim podemos definir que:
Agora só precisamos definir , que nada mais é que a área entre os pontos A e K, e isso que vamos ver no próximo passo.
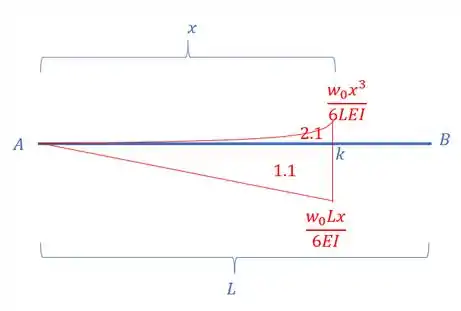
Assim podemos definir que:
E igualando, temos que:
Podemos definir que:
Assim teremos que:
Resolvendo a nossa função, teremos que:
Sabemos que valores negativos e maiores que 1 não fazem sentido para nós, assim, temos que:
Assim temos que: