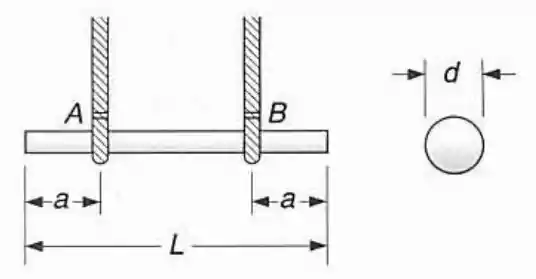
Uma barra de aço uniforme de diâmetro é içada por cabos de um guindaste, amarrados em e . Pede-se: (a) determinar a distância , entre as extremidades da barra e os pontos onde os cabos estão atados, para que o máximo valor absoluto do momento fletor na viga seja o menor possível; (b) determinar a correspondente tensão normal máximadevido à flexão, sabendo-se que e e que para o aço . (Veja a sugestão do Prob. 7.31)
Passo 1
Para resolver esse problema a gente tem que entender que conforme a distância varia o nosso diagrama de momento fletor varia também. Quando é muito pequeno ou muito grande o momento fletor máximo acaba ficando grande.
Logo, existe um ponto onde o maior momento fletor na barra é mínimo e é esse ponto que queremos achar.
Como a barra esta sustentada pelos dois cabos de forma simétrica cada cabo suportará metade do peso. Vamos definir o peso por unidade de comprimento como assim o peso total será e vamos ter a seguinte configuração da barra:
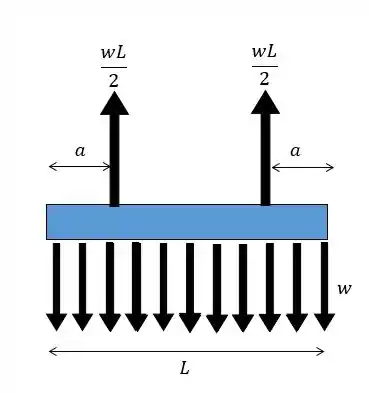
Com isso a gente vai poder desenhar o momento fletor e achar o valor de forma que o momento fletor seja mínimo, vamos lá!
Passo 2
Vamos calcular a cortante e o momento fletor para cada seção da barra. Para a primeira parte vamos ter:
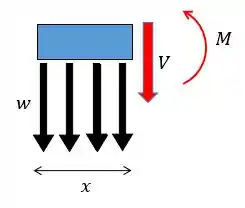
Assim, podemos calcular a força cortante:
E o momento fletor:
No ponto vai valer:
Passo 3
Agora para a seção intermediária:
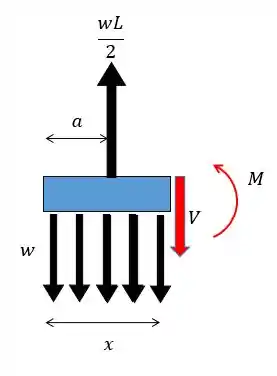
A força cortante é calculada como:
E o momento fletor:
Reorganizando:
No ponto médio vale:
Passo 4
Agora vamos fazer o diagrama de momento fletor:
Para :
Para :
Para :
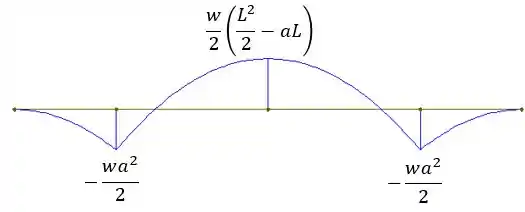
A gente pode observar que os pontos máximos são em e . (Também tem o ponto mas o valor vai ser o mesmo de então não precisamos nos preocupar com esse ponto).
Para que tenhamos um valor mínimo a gente tem que dividir esses momentos máximos (absolutos) igualmente, ou seja, os dois valores devem ser iguais. Assim,
Simplificando:
Aí a gente aplica bhaskara:
Como deve ser positivo:
Pronto, resolvemos a letra A
Passo 5
Agora para a letra B basta substituir os valores, como os momentos fletores são iguais:
Calculando
Calculando :
Substituindo:
Passo 6
Mas o problema não pediu o momento fletor, pediu a tensão. Então aplicando a equação da tensão normal:
E o momento de inércia é dado por:
Assim, vamos ter:
Resposta
a)
b)