Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 94

Para a viga com o carregamento mostrado, determinar a reação no apoio móvel e a deflexão no ponto c.

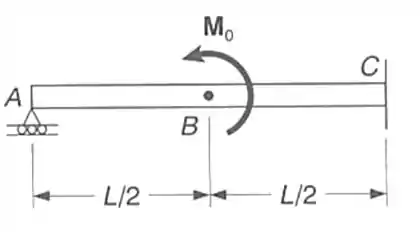
Passo 1

E ai gurizada tudo belezinha??? Vamos analisar a viga em questão...antes vamos desenhar o diagrama de corpo livre....Note que podemos dividir em 3 situações diferentes pois temos rótula, momento e a reação RB, então para isso vamos fazer 3 DCL para analisa-los vem comigo :D

Agora vamos estudar o caso 1 as relações abaixo você encontra no apêndice D do livro ;)

Y b =   - R b L 3 3 E I e ∅ b =   - R b L ² 2 E I

Agora vamos desenhar o DCL para o 2º caso :D

As relações abaixo você encontra no apêndice D do livro

Y b =   M b L 3 2 E I e ∅ b =   M b L E I

Agora vamos desenhar o DCL para o 3º caso :D

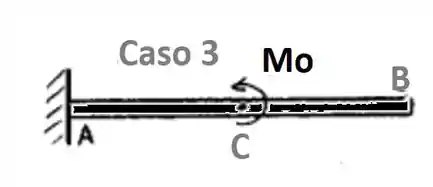
Y b =   M 0 ( L 2 ) 2 2 E I =   3 M 0 L ² 8 E I             e ∅ b =   M o L 2 E I

Vamos fazer o somatório das equações da linha elástica...

Y b = Y b 1 + Y b 2 + Y b 3 = 0  

Y b = - R b L 3 3 E I + M b L 3 2 E I + 3 M 0 ² 8 E I = 0  

Também vamos realizar o somatório das rotações nos apoios

∅ b = ∅ b 1 + ∅ b 2 + ∅ b 3

∅ b = - R b L ² 2 E I +   M b L E I +   M o L 2 E I

Isolando a reação em b (RB temos):

R B = 3 M o 2 L

E para o momento em b (Mb) tem-se:

M B = M o 4

Resposta

R B = 3 M o 2 L

M B = M o 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Antes da carga P ser aplicada, uma abertura δ 0 = 6,35m m existe entre a viga de perfil laminado de aço S 75 × 8,5 e o apoio B. Sabendo-se que E = 200G P a , determinar a intensidade de P para que a d
A viga uniforme ABC suporta uma carga vertical de 40 k N aplicada no ponto C, como mostrado. Usando E = 200 G P a , determinar:A declividade em C
A viga uniforme ABC suporta uma carga vertical de 40 k N aplicada no ponto C, como mostrado. Usando E = 200 G P a , determinar:A deflexão em C
Para a viga com o carregamento mostrado, determinar:A declividade em A
Para a viga com o carregamento mostrado, determinar a deflexão:No ponto médio C do vão AB; Usar E = 200 G P a