Antes da carga ser aplicada, uma abertura existe entre a viga de perfil laminado de aço e o apoio B. Sabendo-se que , determinar a intensidade de para que a deflexão em A seja de .
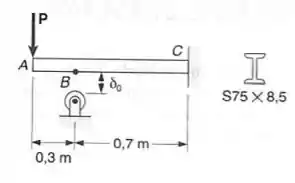
Passo 1
Nosso objetivo é determinar a deformação em A, assim sabemos que a nossa viga é dada por:
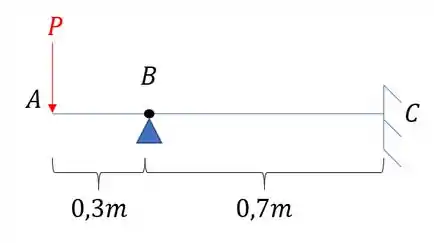
Vamos dividir a nossa viga em duas partes e com isso vamos romper o apoio em B e vamos trocar por uma reação.
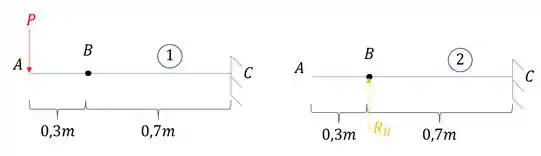
Passo 2
- Deformação no ponto A na viga 2
- Deformação no ponto A na viga 1
- Deformação no ponto B na viga 2
- Deformação no ponto B na viga 1
Sabemos que a tabela no fim do livro é dada por:
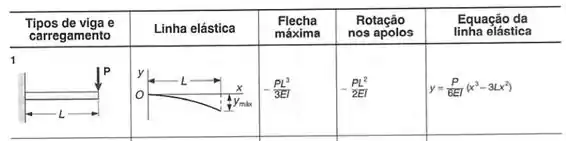
Considerando a deformação no ponto B, podemos considerar o ponto que está a carga como o fim da viga engastada, assim, podemos aplicar a seguinte equação:
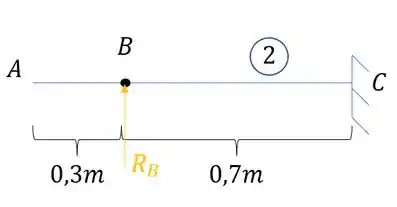
Como a nossa carga é de baixo pra cima, podemos considerar a deformação como sendo positiva.
Como queremos a deformação em A, podemos fazer o seguinte:
Sabemos que a tabela no fim do livro é dada por:
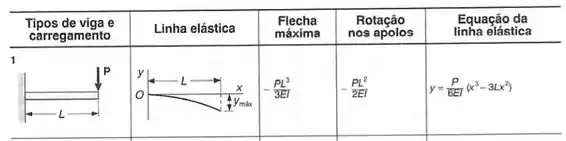
E termos a nossa viga onde usaremos
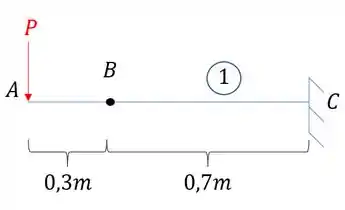
Assim temos que a reação em A é dada por:
Sabemos que podemos fazer o seguinte isolamento:
Olhando a deformação em B, temos a seguinte relação:
Sabemos que a tabela no fim do livro é dada por:
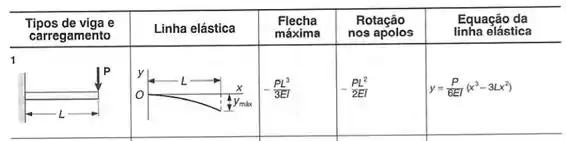
Considerando a deformação no ponto B, podemos considerar o ponto que está a carga como o fim da viga engastada, assim, podemos aplicar a seguinte equação:
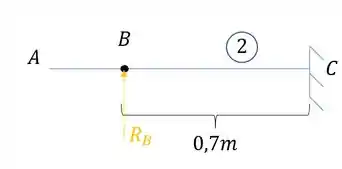
Como a nossa carga é de baixo pra cima, podemos considerar a deformação como sendo positiva.
Sabemos que a tabela no fim do livro é dada por:
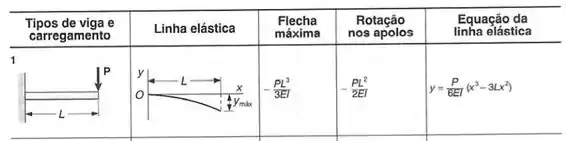
E termos a nossa viga onde usaremos
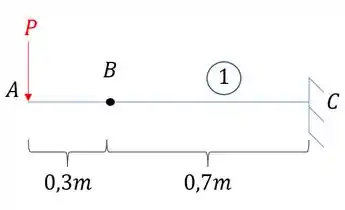
Assim temos que:
Agora temos que lembrar do que eu falei lá no início, antigamente dizíamos que a soma dessas deformações deveria ser zero, mas aqui, pelo contrário, diremos que a soma tem que ser igual ao intervalo de deformação que ocorre no ponto B da nossa viga pode ter, ou seja, , que em metros é dado por , e lembra que essa deformação pra baixo é negativa, assim teremos que:
Substituindo na nossa equação antes das deformações, temos que:
Calculando , temos que:
E o momento de inércia pelo fim do livro é dada por:
Assim temos que:
Substituindo temos que: