Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 9

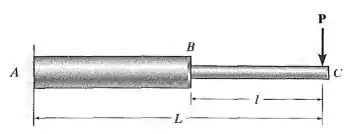
A viga é composta por duas hastes e está sujeita à carga concentrada P. Determine a deflexão máxima da viga, se os momentos de inércia das hastes forem IAB e IBC e o módulo de elasticidade for E.

Passo 1

Para 0 ≤ x 1 ≤ 1 :

M x 1 = - P x 1

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2 v 1 d x 1 2 = - P x 1

E I d v 1 d x 1 = - P 2 x 1 2 +   C 1

E I v 1 = - P 6 x 1 3 + C 1 x 1 + C 2

Para l ≤ x 2 ≤ L :

M x 2 = - P x 2

Logo:

E I d 2 v 2 d x 2 2 = - P x 2

E I d v 2 d x 2 = - P x 2 2 2 + C 3

E I v 2 = - P 6 x 2 3 + C 3 x 2 + C 4

Passo 2

As condições de contorno serão:

x 2 = L → v 2 = d v 2 d x 2 = 0

x 1 = x 2 = l → v 1 = v 2   e     d v 1 d x 1 = d v 2 d x 2

Logo, substituindo:

C 1 = I b c I a b - P l 2 2 + P L 2 2 ; C 2 = I b c I a b P l 3 3 - P L 3 3 - P l 3 3 ; C 3 = P L 2 2 ; C 4 = - P L 3 3

Passo 3

Logo:

v 1 = 1 E I b c - P x 1 3 6 + I b c I a b - P l 2 2 + P L 2 2 + P l 2 2 x 1 + I b c I a b P l 3 3 - P L 3 3 - P l 3 3

Portanto, em x 1 = 0 :

v m á x = P 3 E I a b 1 - I a b I b c l 3 - L 3

Resposta

v m á x = P 3 E I a b 1 - I a b I b c l 3 - L 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando o método da Seção 5.2 , resolva o Problema 5.20 .Para a viga e o carregamento mostrados, determine a tensão normal máxima provocada pelo momento fletor na seção transversal C .
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.
Determine ( a ) as equações das curvas de força cortante e momento fletor para a viga e o carregamento mostrados na figura e ( b ) o valor máximo absoluto do momento fletor na viga.
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados e, determine a tensão normal máxima provocada pelo momento fletor.