Usando as técnicas descritas no Apêndice A, Exemplo A.5 ou A.6, a seção em Z tem momentos principais de inércia Iy= 0,060(10-3)m4 e Iz= 0,471(10-3)m4, calculados em torno dos eixos principais de inércia y e z, respectivamente. Se a seção for submetida a um momento interno
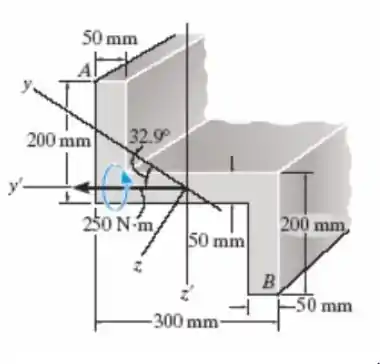
M = 250 N · m direcionado na horizontal, como mostra a figura, determine a tensão produzida no ponto A.
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? A questão de hoje tem essa cara meio estranha e formal, mas ele enrolou só pra dizer que os momentos de inércia, nos eixos y e z, são aqueles dados, e um momento M foi aplicado formando um ângulo de 32,9º em relação ao y com a horizontal. Depois desse monte de número, vamos determinar a tensão no ponto A. E aí, preparados?? Bora lá!
Passo 2
Primeira coisa que vamos fazer aqui é desenhar. Esse monte de eixo, coordenadas, ângulos e números tá tudo bagunçado. Vamos usar a geometria analítica para encontrar a equação da reta para achar as coordenadas de A, já que os eixos estão fora do eixo (entenderam a piada?? Kkkkk Não?? Ok, vamos voltar). Vamos traçar uma reta paralela ao eixo y que passa por A.
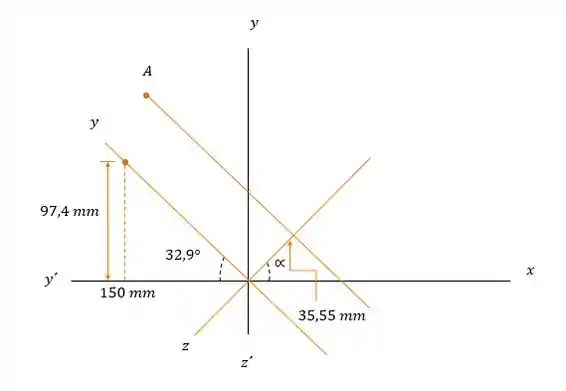
Reta que passa por e
Reta que passa por e
Reta com
Para acharmos a intersecção com o eixo x, vamos igualar
Assim, para acharmos o valor da intersecção de y, vamos substituir em
Agora, depois de tanta reta de um lado pro outro, vamos fazer o módulo da distância entre o ponto A e a intersecção com y, nos dando sua nova coordenada.
Para a coordenada em z, é só a gente dividir pelo cosseno do ângulo entre as retas
Passo 3
Depois de acharmos esses mil passos para as coordenadas de A, vamos jogar esses valores nas equações da decomposição do momento, para sabermos quanto vale cada uma de suas componentes.
Sabemos que a tensão resultante será a soma de cada uma das componentes dos momentos de cada eixo. Sendo assim: