Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 32

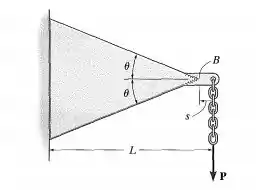
A viga cônica mostrada na figura tem largura constante b . Se ela suportar uma carga P em sua extremidade, determine a deflexão B . A carga P é aplicada a uma curta distância s da extremidade B , onde s ≪ L . E I   é constante.

Passo 1

Primeiro, temos:

M x = P x

Para I :

I = b 2 x tan ⁡ θ 3 12 I = 2 3 ( b tan 3 ⁡ θ x 3 )  

E que o momento é dado por:

∑ M = 0 M x = P x

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2   v d x 2 = P x

d 2   v d x 2 = P x E I

d 2   v d x 2 = 3 P 2 E 2 3 b tan 3 ⁡ θ x x 3 = k x 2

k = 3 P 2 E tan 3 ⁡ θ

d v d x = - k 1 x +   C 1

v = - γ h 2 E x 2 + C 1 x + C 2

Passo 2

Sabemos que:

E I d 2 v 1 d x 1 ² = M x

Logo:

E I d 2   v d x 2 = P x

d 2   v d x 2 = P x E I

d 2   v d x 2 = 3 P 2 E 2 3 b tan 3 ⁡ θ x x 3 = k x 2

k = 3 P 2 E tan 3 ⁡ θ

d v d x = - k 1 x +   C 1 para x = L → d y d x = 0

Assim, temos:

C 1 = k L

Para encontrarmos C 2 :

y = - k ln ⁡ x + k L x + C 2 para x = L → y = 0

Com isso:

C 2 = k ( ln ⁡ L - 1 )

Passo 3

Por fim, vamos substituir. Fica assim:

y = - k ln ⁡ x + k L x + k ln ⁡ L - 1 , para x = s → y = - k ln ⁡ s + k s L + k ln ⁡ L - 1

Logo:

L ≫ s

E

y = k ln ⁡ L s - k

y = 3 P 2 E b tan 3 ⁡ θ ln ⁡ L s - 1

Resposta

y = 3 P 2 E b tan 3 ⁡ θ ln ⁡ L s - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo-se que a viga A B é feita de uma barra maciça de aço, com diâmetro d = 20 m m , determinar para o carregamento mostrado:A Deflexão no ponto A
Resolver o P r o b . 9.53 , considerando que a força de 670 N em A, atua para baixo.A declividade no ponto E
Resolver o P r o b . 9.53 , considerando que a força de 670 N em A, atua para baixo.A Deflexão no ponto A
Resolver o P r o b . 9.53 , considerando que a força de 670 N em A, atua para baixo.A declividade no ponto D
Sabendo-se que a viga A B é feita de uma barra maciça de aço, com diâmetro d = 20 m m , determinar para o carregamento mostrado:A declividade no ponto D