Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 42

Uma viga consiste em cinco pranchas de seção transversal 40   x   150 m m , conectadas por parafusos de aço, com espaçamento horizontal de 230   m m . Sabendo-se que o cisalhamento na viga é vertical e igual a 8900   N e que a tensão de cisalhamento admissível em cada parafuso é de 50   M p a , determinar o menor diâmetro necessário dos parafusos.

Passo 1

Queremos determinar a máxima força que age em cada um dos parafusos, sabemos que a carga por metro é determinada da seguinte maneira

q = V Q I

E como queremos a força que age em cada parafuso, precisamos multiplicar a carga por metro pela distância entre parafusos, sendo assim teremos que:

F = q s

Sendo “s” a distância entre parafusos também sabemos que:

V = c o r t a n t e   a g i n d o   n a   s e ç ã o  

Q = m o m e n t o   e s t á t i c o  

I = m o m e n t o   d e   i n é r c i a  

s = 23 0   m m

τ A D M = 50   M p a

Agora precisamos determinar o momento estático e o momento de inércia, para isso temos um passo a passo.

Passo 2

Vamos primeiro encontrar a LN do nosso problema, para isso sabemos que a nossa fórmula é dada por:

y ¯ = ∑ A i y i ∑ A i

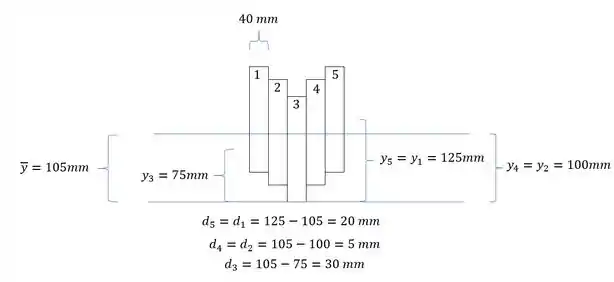
Sabemos que devemos calcular as áreas e Y com relação a uma origem determinada, com isso podemos usar a seguinte figura e a seguinte tabela:

y ¯ = 3150000 30000 = 105   m m

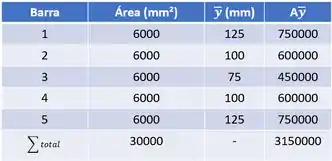
Assim a LN será dada por:

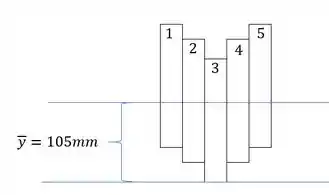
Passo 3

Vamos determinar primeiro o momento de inércia, para isso precisamos determinar algumas coisas, para isso temos que fazer o seguinte passo a passo.

  • Primeiro determinamos uma divisão em seções mais simples

  • Em segundo determinamos as áreas da nossa seção

  • Em terceiro determinamos a distância dos centroides dos elementos até a LN, e como a seção é simétrica, está no centro da seção total, sendo assim teremos que:

  • Em quarto precisamos determinar os momentos de inércia de cada uma das seções mais simples:

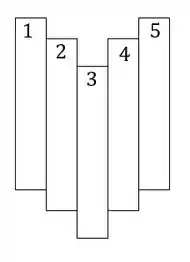
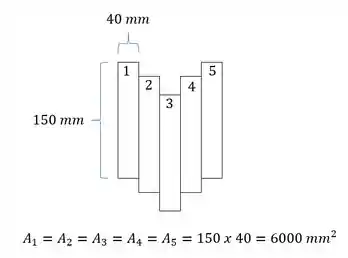
    • Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:

    I = ∑ I i + A i d i 2

    Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:

    I = I 1 + A 1 d 1 2 + I 2 + A 2 d 2 2 + I 3 + A 3 d 3 2 + I 4 + A 4 d 4 2 + I 5 + A 5 d 5 2

    I = 11250000 + 6000   .   20 2 + 11250000 + 6000   .     5 2 + 11250000 + 6000   .     30 2 + 11250000 + 6000   .   5 2 + 11250000 + 6000   .     20 2

    I = 66750000   m m 4

    Passo 3

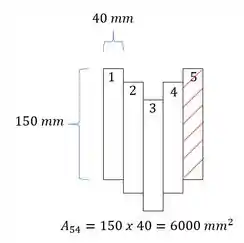
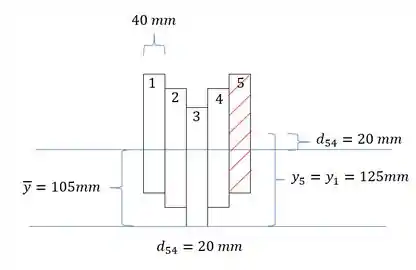
    Aqui precisamos ver duas seções principalmente, vamos ver a seção entre a seção 5 e 4, sendo assim teremos que:

  • Área da seção cisalhada:

  • Distância do centroide da área até a LN

    • Q 54 = A 54 y 54   = 6000   .     20 = 120000   m m 3

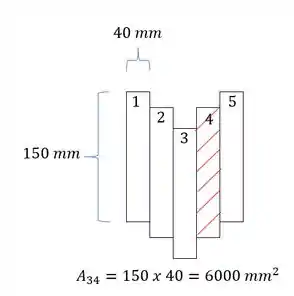
    Vendo agora a seção entre 3 e 4

  • Área da seção cisalhada:

  • Distância do centroide da área até a LN : e aqui vale ter um cuidado, perceba que agora a distância do centroide da área está ABAIXO da LN, ou seja, esse valor deve ser negativo no cálculo, sendo assim teremos que:

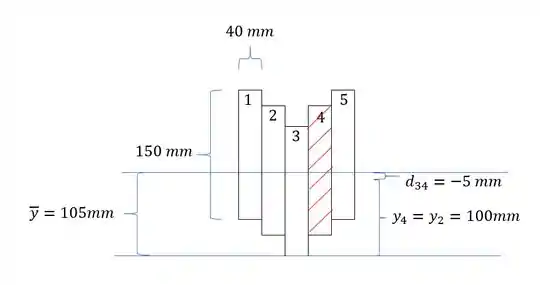
    • Outra coisa, lembre-se que o parafuso foi solicitado na seção 4 e 5, logo, precisamos somar essa contribuição, sendo assim teremos que:

    Q 3 4 = Q 54 + A 3 4 y 3 4   = 120000 + 6000   .   ( - 5 ) = 90000   m m 3

    Logo, a seção mais solicitada é a que tem:

    Q 54 = A 54 y 54   = 6000   .     20 = 120000   m m 3

  • Assim podemos determinar a máxima carga por metro que podemos ter:

Sabemos que:

V = 8900   N

Q = 120000   m m 3

I = 66750000   m m 4

q = V Q I = 8900     .     120000     66750000 = 16 N m m

Multiplicando isso pela distancia entre os parafusos teremos que:

F = q S = 16   .   230 = 3680   N  

Queremos saber o diâmetro do parafuso, e sabemos que:

τ p a r a f u s o = F A = 3680 π D 2 4 = 4   .   3680 π D 2 = 50   M P a

D 2 = 4   .   3680 π 50

D 2 = 93,71

D = 93,7 1 = 9,68   m m

Resposta

D = 9,68   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três pranchas são conectadas como mostrada, por parafusos de 16 m m de diâmetro e espaçados de 300m m , ao longo do eixo longitudinal da viga. Para uma força cortante vertical de 13350N , determinar a
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.