Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 108

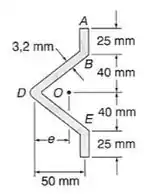
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.

Passo 1

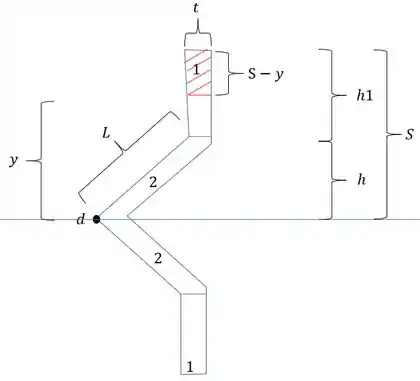
Para esse tipo de questão sabemos que a nossa tensão de cisalhamento produz na seção forças que são decorrentes do diagrama de tensões. Mas ai temos o seguinte macete, imagine que na verdade a nossa seção tenha o seguinte fluxo de tensões.

Se calcularmos o momento fletor em torno de “d” teremos que:

M d = 2 F b

Agora pensa o seguinte, se temos esse momento fletor agindo em torno de “d” vamos tentar equilibrar ele, e para equilibrar, precisamos descobrir qual a distância “e” que podemos colocar a nossa carga vertical para garantir que a nossa seção vá descer vertical, e não rotacionar, sendo assim, teremos que:

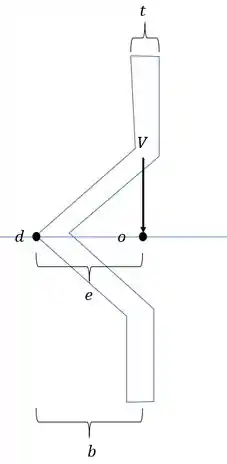
Calculando o momento fletor em “d” teremos que:

M d = V e

E igualando os momentos fletores, teremos que:

V e = 2 F b

e = 2 F b V

Sabemos que a força que age na seção superior e gera a força F é dada pela seguinte equação:

F = ∫ τ d A

Sabemos que:

τ = V Q I b

Precisamos determinar o momento de inércia total da nossa seção, vamos seguir o seguinte passo a passo.

Passo 2

Vamos determinar primeiro o momento de inércia, para isso precisamos determinar algumas coisas, para isso temos que fazer o seguinte passo a passo.

para determinarmos o momento de inércia, precisamos fazer a seguinte conta:

I = ∑ I i + A i d i 2

  • Primeiro determinamos uma divisão em seções mais simples

  • Em segundo determinamos as áreas da nossa seção

  • Em terceiro determinamos a distância dos centroides dos elementos até a LN, e como a seção é simétrica, está no centro da seção total, sendo assim teremos que:

  • Em quarto precisamos determinar os momentos de inércia de cada uma das seções mais simples:

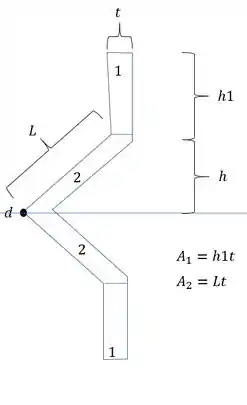
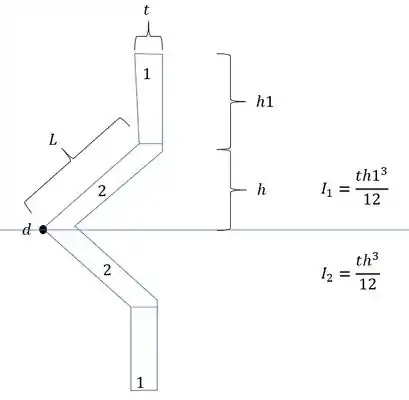
    • Agora para determinarmos o momento de inércia, precisamos fazer a seguinte conta:

    I = ∑ I i + A i d i 2

    Mas temos que lembrar que precisamos usar os valores de inercia da região 6 como negativa, sendo assim temos que:

    I = 2 ( I 1 + A 1 d 1 2 ) + 2 ( I 2 + A 2 d 2 2 )

    I = 2 t h 1 3 12 + h 1 t   .     h 1 2 + h 2 + 2 t h 3 12 + L t   . h 2 2

    O termo com t 3 podemos ignorar, sendo assim teremos que:

    I = 2 t h 1 3 12 + h 1 t   .     h 1 2 + h 2 + 2 t h 3 12 + L t   . h 2 2

    I = 2 t h 1 3 12 + h 1 t   .     h 1 2 + h 2 + 2 t h   .     h 2 12 + L t h 2 4

    Com isso podemos considerar que aproximadamente podemos fazer a seguinte aproximação:

    t h = L t

    Sendo assim teremos que:

    I = 2 t h 1 3 12 + h 1 t   .     h 1 2 + h 2 + 2 L t   h 2 12 + h 2 4

    I = 2 t h 1 3 12 + h 1 t   .     h 1 2 + h 2 + 2 L t   h 2 12 + 3 h 2 12

    I = 2 t h 1 3 12 + h 1 t   .     h 1 2 + h 2 + 2 L t   h 2 12 + 3 h 2 12

    I = 2 t h 1 3 12 + h 1 t   .     h 1 2 + h 2 + 2 L t h 2 3

    Assim sabemos que:

    t = 3,2   m m

    h = 4 0   m m

    h 1 = 25   m m

    b = 5 0   m m

    L = b 2 + h 2 = 40 2 + 50 2 = 64   m m

    I = 2 3,2   .     25 3 12 + 25   .     3,2   .     25 2 + 40 2 + 2 64   .     3,2   .     40 2 3 = 667787   m m 4

    Passo 3

    Para o momento estático, precisamos escrever a nossa equação em função disso, porque sabemos que a nossa força está em função da tensão, sendo assim podemos fazer o seguinte:

  • Área da região acima do ponto que se quer saber o cisalhamento

    • A = t ( S - y )

    Lembrando que x é a variação do comprimento da área analisada.

  • Distância do centroide da área até a LN

    • y 1 = S + y 2

    agora para determinar o momento estático precisamos fazer a seguinte conta:

    Q = A 1 y 1 = t S - y S + y 2 = t 2 ( S 2 - y 2 )

    E sabemos que a espessura de cisalhamento é dado por “t”. substituindo isso na nossa equação teremos que:

  • Tensão

τ = V Q I b = V   .   t 2 ( S 2 - y 2 )     I     .   t

Sabemos que devemos substituir isso na seguinte integral:

F = ∫ τ d A

Sabemos que:

A = t ( S - y )

Logo:

d A = - t d y

Sendo assim teremos que:

F = ∫ V   .   t 2 ( S 2 - y 2 )     I     .   t ( - t d y )

F = ∫ V   .   ( S 2 - y 2 )     2 I ( - t d y )

F = - V t 2 I ∫ ( S 2 - y 2 ) ( d y )

F = - V t 2 I S 2 y - y 3 3

Como sabemos que y varia de 40 até 65, podemos ignorar o zero e analisar apenas o 40, sendo assim teremos que:

t = 3,2   m m

S = h 1 + h = 40 + 25 = 65 m m

I = 667787   m m 4

F = - V   .     3,2 2   .     667787 65 2 65 - 65 3 3 - 65 2 40 - 40 3 3 = - 0,0849 V  

Mas lembra o nosso objetivo? Queremos determinar a excentricidade que podemos aplicar a nossa carga, sendo assim, teremos que:

e = 2 F b V = 2   .   - 0,0849 V   .     50 V = - 8,49   m m

Resposta

e = - 8,49   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o P r o b . 5.37 , considerando que a viga seja submetida a uma força cortante horizontal V .
Uma viga extrudada tem a seção transversal mostrada e uma espessura constante da parede de 5 m m . Sabendo-se que uma dada força vertical V causa uma tensão de cisalhamento máxima igual a 60M P A , de
Resolver o P r o b . 5.36 , considerando que a viga seja submetida a uma força cortante horizontal V .
Quatro perfis de aço cantoneira 102 x 102 x 9,5 e uma placa de aço de 12 x 40 0m m são aparafusadas juntas para formar uma viga como a seção transversal mostrada. Os parafusos são de 22 m m de diâmetr
Resolver o Prob.5.40, considerando que a altura da placa é aumentada de 400m m para 600 m m .