Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 120

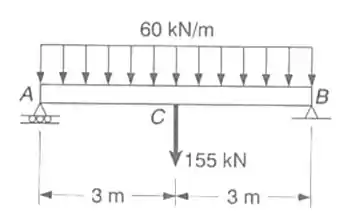
Para a viga constituída de um perfil laminado de aço W610 x 101 e o carregamento mostrado, determinar: a) a declividade na extremidade A b) deflexão no ponto médio C. Usar E= 200 GPa

Passo 1

E ai gurizada tudo belezinha??? Vamos analisar a viga em questão...

Antes vamos extrair as informações do enunciado vem comigo :D Notem que temos 2 cargas faremos então para a distribuída primeiramente :D

W= 60 KN/m , L= 6 m , x= 3m

Agora para determinarmos a declividade no ponto A usaremos a equação abaixo :D (lembrando que essas equações variam de uma viga para outra, e s encontram em anexo no livro).

  1. ∅ a =   - w L 2 24 E I

    2. ∅ a =   - 60 × 6 2 24 E I = - 2160 24 E I

    Y b =   - w 24 E I × x 4 - 2 L x 3 + L 3 x = - 60 24 E I × 3 4 - 2 × 6 × 3 3 + 6 3 × 3 =   - 2025 2 E I

    I= 762 x 106 mm4 = 762 x 10-6 m4 E= 200 x 109

    Então para EI temos:

    E I = 200   x   10 9 × 762   x   10 6 = 152,4 x   10 6   N m ²  

    Passo 2

    Para a carga concentrada de 155 KN a= 3m, b= 3m x=a 3m

  2. ∅ a =   - P b   L 2 - b 2 6 E I L = - 155 × 3   6 2 - 3 2 6 E I × 6 = 4185 4 E I

Y b =   - P a 2 b 2 3 E I L = - 155 × 3 2 × 3 2 3 E I × 6 = - 1395 2 E I

Passo 2

Calculando a relação EI para substituirmos nas equações acima temos:

I= 762 x 106 mm4 = 762 x 10-6 m4 E= 200 x 109

Então para EI temos:

E I = 200   x   10 9 × 762   x   10 6 = 152,4 x   10 6   N m ²  

  1. Declividade: ∅ a = - 2160 24 E I + 4185 4 E I = - 2160 24 × 152,4 x   10 6 + 4185 4 × 152,4 x   10 6 = - 5,9 × 10 - 7 + 6,86 × 10 - 6 = 6,275 × 10 - 6   r a d
  2. Deflexão:   Y b = - 1395 2 E I   - 2025 2 E I = - 1395 2 × 152,4 x   10 6   - 2025 2 × 152,4 x   10 6 = - 1,122 × 10 - 5 m

Resposta

a )   ∅ a = 6,275 × 10 - 6   r a d

b )   Y b = - 1,122 × 10 - 5 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que a viga A B é um perfil de aço laminado S 200 × 34 e que P = 60k N , L = 12m m e E = 200G P a , determine ( a ) a inclinação em A e ( b ) a deflexão em C .
Para o carregamento mostrado nas figuras, determine ( a ) a equação da linha elástica para a viga em balanço A B , ( b ) a deflexão da extremidade livre e ( c ) a inclinação na extremidade livre.
Para a viga em balanço e o carregamento mostrados nas figuras, determine ( a ) a equação da linha elástica para a parte A B da viga, ( b ) a deflexão em B e ( c ) a inclinação em B .
Para o carregamento mostrado nas figuras, determine ( a ) a equação da linha elástica para a viga em balanço A B , ( b ) a deflexão da extremidade livre e ( c ) a inclinação na extremidade livre.
Para o carregamento mostrado nas figuras, determine ( a ) a equação da linha elástica para a viga em balanço A B , ( b ) a deflexão da extremidade livre e ( c ) a inclinação na extremidade livre.