Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 65

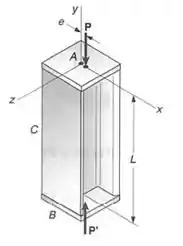
Cargas axiais de intensidade P= 90 KN são aplicadas paralelamente ao eixo geométrico do perfil laminado de aço w 250 x 80 da coluna AB e interceptam o eixo x a uma distância e do eixo geométrico. Sabendo-se que σ a d m = 170   M P a e E= 200 GPa, determinar o maior comprimento permissível L, quando a) e= 6,35 mm b) e= 12,7 mm

Passo 1

E ai gurizada tudo belezinha??? Vamos analisar a viga em questão... e vamos pegar algumas informações dessa viga no apêndice....

A =   10200   m m 2 = 10200   × 10 - 6   m ²

I =   43,1   × 10 - 6   m 4

b f =   255   m m

c = b f 2 =   255 2 = 127,5   m m  

r y = 65   m m

σ a d m = 170   × 10 6 P a

Passo 2

  1. Gurizada agora temos que definir a equação a ser utilizada

    2. σ m á x = P A   ( 1 + ec r 2 ( sec ⁡ π 2 × P P s   ) )

    Isolando ( sec ⁡ π 2 × P P s   ) temos:

    ( sec ⁡ π 2 × P P s ) = r 2 e c × A σ m á x P - 1

    ( sec ⁡ π 2 × P P s ) = 65 ² 6,35 × 127,5 × 10200   × 10 - 6 × 170   × 10 6 90 × 10 3 - 1

    ⁡ π 2 × P P s ) = 48,75

    P P s = 2 π × 48,75   2 = 963,18

    P s = P 963,18 = π 2 E I L 2

    L 2 = 963,18 × π 2 E I P

    L 2 = 963,18 × π 2 × 200 × 10 9 ×   43,1   × 10 - 6 90 × 10 3

    L = 9,1   m

    Passo 3

  2. Para a excentricidade de e= 12,7 mm os cálculos são os mesmos vem comigo :D

( sec ⁡ π 2 × P P s ) = 127,5 ² 12,7   × 127,5 × 10200   × 10 - 6 × 170   × 10 6 90 × 10 3 - 1

⁡ π 2 × P P s ) = 0 , 650  

P P s = 2 π × 0650 2 = 0 , 171

P s = P 0 , 171 = π 2 E I L 2

L 2 = 0 , 171 × π 2 E I P

L 2 = 0 , 171 × π 2 × 200 × 10 9 ×   43,1   × 10 - 6 90 × 10 3

L = 12,7   m

Resposta

A ) 9,1   m

b )   12,7   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

σ c = 8,3 M P a e um módulo de elasticidade ajustado E = 11,1G P a . Usando o método da tensão admissível, determine o maior comprimento de flambagem L admissível que pode ser usado.
σ c = 8,3 M P a e um módulo de elasticidade ajustado E = 11,1G P a . Usando o método da tensão admissível, determine o maior comprimento de flambagem L admissível que pode ser usado.10.100: Resolva o
E = 200 G P a e σ E = 250 M P a .
L 4 × 3 × 3 8 in. de aço são soldadas juntas de modo a formar a coluna AB. Uma carga axial P de intensidade 14kips é aplicada no ponto D. Utilizando o método das tensões admissíveis, determine o maior
10.108: Resolva o problema 10.107 considerando e = 40m m . b igual a 90 mm, 140 mm e 240 mm. Essa madeira tem uma tensão admissível ajustada à compressão paralela às fibras σ C = 8,1M P a e módulo de