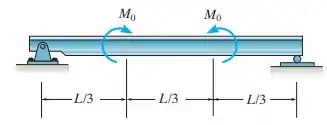
Se , a viga falhará quando a força cortante máxima for ou o momento fletor máximo for . Determine a intensidade do maior momento de binário que a viga suportará.
Passo 1
Fala aí, galera. Beleza? Bora para mais uma questão de Mecânica. Primeiro, vamos começar esboçando o :
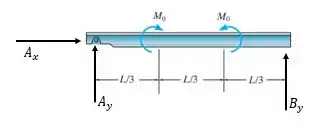
Passo 2
Em seguida, utilizar as equações de equilíbrio para determinarmos as reações de apoio:
Para o eixo , temos:
E para o momento, temos:
Logo:
Passo 3
Para determinarmos os esforços cortantes e os momentos fletores para esboçarmos cada diagrama precisamos dividir a nossa viga em porções. Para a primeira, , temos que o DCL vai ser:
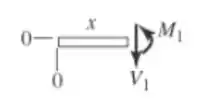
Pelas equações de equilíbrio, temos:
Para o momento, temos:
Passo 4
Vamos repetir o processo, selecionando a porção restante da viga, ou seja, . Vamos esboçar o DCL:
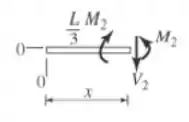
Com isso, vamos utilizar as equações de equilíbrio para determinarmos a força cortante e o momento fletor. Temos:
Para o momento, temos:
Passo 5
Novamente, vamos repetir o processo, selecionando a porção restante da viga, ou seja, . Vamos esboçar o DCL:

Com isso, vamos utilizar as equações de equilíbrio para determinarmos a força cortante e o momento fletor. Temos:
Para o momento, temos:
Passo 6
Com isso, sabemos que a força de cisalhamento é zero em todos os pontos da viga. E que O momento é zero no primeiro terço e no último terço da viga. Logo, o momento máximo vai ocorrer na seção intermediária. E a gente já o determinou, logo:
Opa, é isso, galera. Bora praticar mais!!!