Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 6.Problemas fundamentais - Ex. 20

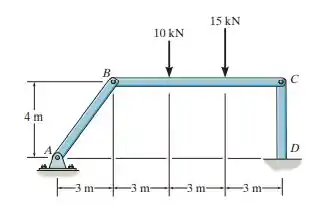
Determine as reações em D .

Passo 1

Fala, galera. Beleza? Bora para mais um exercício de Mecânica. Para determinarmos as reações em D , vamos primeiro esboçar o DCL para a barra C D :

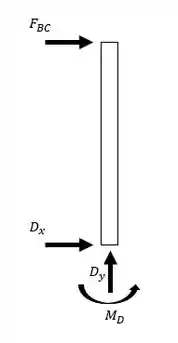
Passo 2

Com o DCL em mãos, é possível determinar o módulo da força F_A B para determinar as reações em C restantes. Então, pelas reações de equilíbrio, temos:

sum M_C = 0 400 (2) + 500 (1) - F_A B ((1,2)/(1,5)) (3) = 0 F_A B = 541,67 N

Passo 3

Com isso, com o valor de F_A B é possível fazer o equilíbrio de forças para os eixos coordenados e determinar as reações. Logo, para o eixo x :

sum F_x = 0 - C_x + F_A B ((0,9)/(1,5)) = 0 C_x = 470,60 N

E para o eixo y , temos:

sum F_y = 0 C_y = + F_A B ((1,2)/(1,5)) - 400 - 500 = 0 C_y = 466,67 k N

Opa, é isso, galera. Bora praticar mais!!!

Resposta

C_x = 470,60 N

C_y = 466,67 k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força criada nos cilindros hidráulicos E F e A D a fim de manter a caçamba em equilíbrio. A carga da caçamba tem massa de 1,25 Mg e centro de gravidade em G . Todos os nós são conectados p
Determine as componentes horizontal e vertical das forças que os pinos em A e B exercem sobre a estrutura.
Se o tambor de 300 kg possui centro de massa no ponto G , determine as componentes horizontal e vertical da força atuando no pino A e as reações sobre os calços lisos C e D . A garra em B no membro D
A estrutura de dois membros é conectada por um pino em E . O cabo é preso a D , passa pelo pino liso em C e suporta a carga de 500 N. Determine as reações horizontal e vertical em cada pino.
Determine a massa necessária do cilindro suspenso se a tração na corrente em volta da engrenagem de giro livre for 2 kN. Além disso, qual é a intensidade da força resultante no pino A?