A viga retangular mostrada na figura é feita de um plástico para o qual o modulo de elasticidade em tração é metade de seu valor em compressão. Para um momento fletor , determine.
- A tensão de tração máxima
- A tensão de compressão máxima.
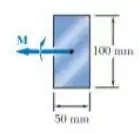
Passo 1
Para essa questão vamos precisar usar o mesmo conceito que já usamos no caso de concreto e aço, mas no nosso caso, temos que lembrar que:
Sabemos que a relação entre módulos de elasticidade é dada por:
Vamos então transformar o trecho em tração e vamos manter intacto o trecho em compressão, assim vamos ter que:
E o que fazíamos com esse fator? Multiplicávamos ele pela largura da nossa seção, certo? Aqui vamos usar um conceito parecido, porém, não igual, porque vamos ter que multiplicar pela área da seção em tração, assim vamos ter que a nossa seção é dada por:
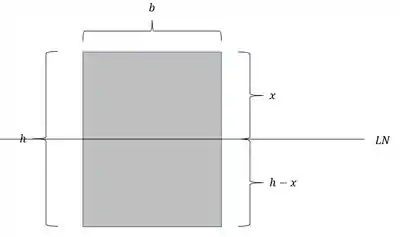
Perceba que ainda não temos a LN, mas como sabemos que ela separa a região em compressão da região em tração, definimos ela em uma posição .
Mas pensa no seguinte, a nossa seção é dada por:
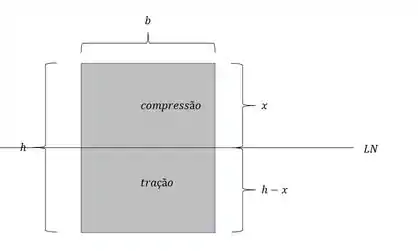
E a LN? É bem simples é só fazer a área de compressão multiplicando pela distancia do centroide dela até a suposta LN, e isso tem que ser igual a área modificada de tração multiplicada pela distância dela a té a suposta LN, assim temos que:
OBS: á área de tração modificada é só pegar a área dela e multiplicar pelo fatro que determinamos lá em cima, assim temos que:
Sabemos então que a altura da nossa seção é de e o valor de que encontramos sendo .
Para o momento de inércia, temos a seguinte equação a ser feita:
e para a tração teremos que:
E porque temos esse temos esse termo de área na equação? PORQUE ESSA ÁREA É A ÁREA MODIFICADA, OU SEJA, TEM QUE TER OBRIGATORIAMENTE O FATOR DE CONVERSÃO, ENTÃO NÃO PODEMOS ESQUECER DE MANEIRA NENHUMA.
Assim teremos que:
Substituindo teremos que:
E agora só precisamos determinar os pontos mais distantes da LN na região de tração e de compressão.
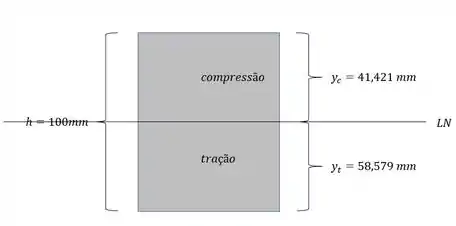
Agora vamos para as nossas tensões.
Passo 2
Nosso objetivo é determinar as tensões, e a fórmula que relaciona a tensão com o momento é dado por:
E se verificarmos a estrutura que foi transformada, no caso a tracionada, teremos que usar a seguinte equação:
Temos então que:
- Verificando a compressão
- Verificando a tração
Assim temos que:
Assim temos que: