Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 89
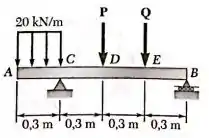
A viga , que está sujeita ao carregamento uniformemente distribuído mostrado na figura e a duas forças desconhecidas e . Sabendo que foi experimentalmente determinado que o momento fletor é em e em , determine e , trace os diagramas de esforço cortante e de momento fletor para a viga.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Primeiro vamos dividir a viga em seções, , e , para facilitar a determinação das cargas e .
O diagrama de corpo livre de está exposto a seguir:
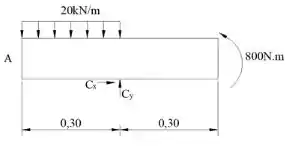
Vamos usar as equações de equilíbrio para encontrar as incógnitas:
Temos também que:
Passo 2
Agora vamos trabalhar na seção :
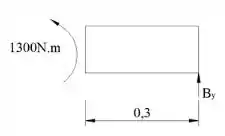
Agora que temos as forças de reação, podemos determinar o valor dos carregamentos de e usando o diagrama do sistema inteiro:
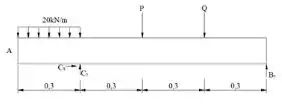
Portanto:
Passo 3
Agora vamos ao diagrama de cortante e momento fletor:
A cortante no ponto é determinada a seguir:
Como no ponto temos a reação de apoio, a cortante no ponto altera, como mostrado a seguir:
A cortante no ponto é determinada a seguir:
A cortante no ponto é dada por:
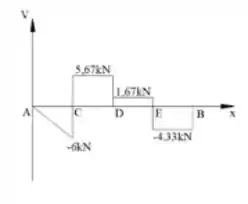
O desenho do diagrama de esforço cortante é mostrado a seguir:
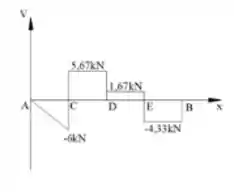
Passo 4
O diagrama de momento fletor é dado pela área abaixo da curva da cortante, entre dois pontos, é igual à variação do momento fletor entre esses pontos. Para o trecho a curva de momento é uma parábola:
Para o trecho o momento fletor é mostrado a seguir:
Para o trecho o momento fletor é dado por:
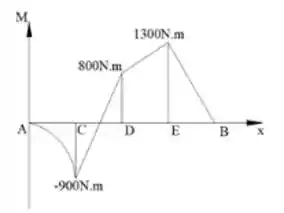
O desenho do diagrama do momento fletor é mostrado a seguir:
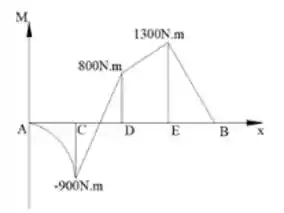
Resposta
