Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 120
Uma viga está sujeita ao carregamento variável mostrado. Calcule as reações de suporte em A e B
Passo 1
A primeira coisa que precisamos fazer é determinar os coeficientes da função de carregamento
Função de carga:
Podemos notar que existem dois coeficientes desconhecidos, então precisaremos escrever duas equações para determiná-los
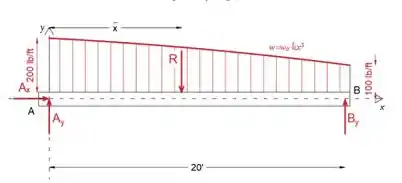
Em x = 0, a intensidade é w = 200, então vamos colocar esses valores na função
Em x = 20, a intensidade é w = 100, então vamos colocar esses valores na função
Substitua por 200
Como determinamos os coeficientes e k, podemos escrever a função de carregamento como:
Passo 2
Uma vez que a intensidade da carga é igual à área sob a curva, determinaremos o R resultante integrando a função parabólica ao longo do intervalo: [0≤x≤20]
Integre o lado direito da equação em relação a dx
Substitua x por 20
Uma vez que a resultante atua no centróide da área, podemos calcular a distância do eixo W como:
Integrando o lado direito da reação com relação a dx
Substitua x por 20
Agora vamos desenhar o diagrama de corpo livre da viga com a carga distribuída substituída pelo R resultante
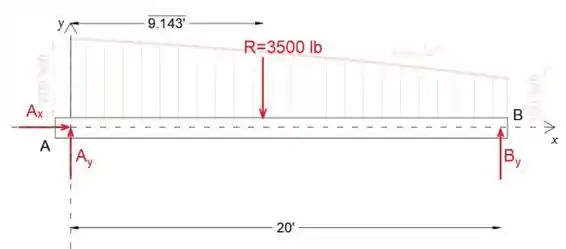
Passo 3
Equacionando a soma das forças na direção x a zero, determinaremos a força de reação Ax
Ao igualar o momento sobre ponto A a zero, podemos determinar a força de reação By
Podemos expressar By como
Equacionando a soma das forças na direção y a zero, determinaremos a força de reação Ay
Substitua R e By por seus valores