Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 142

Desenhe os diagramas de cisalhamento e momento para a viga carregada como mostrado. Especifique o momento máximo M"max"

Passo 1

Nesta tarefa, precisamos desenhar os diagramas de cortante e momento para a viga. Além disso, precisamos determinar os valores do momento fletor máximo

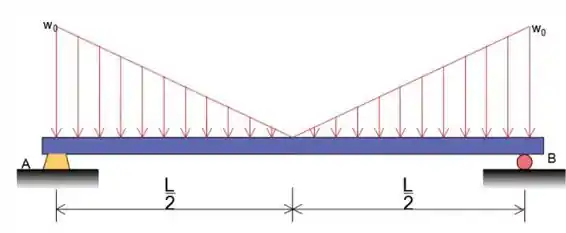
Passo 2

Diagrama de corpo livre

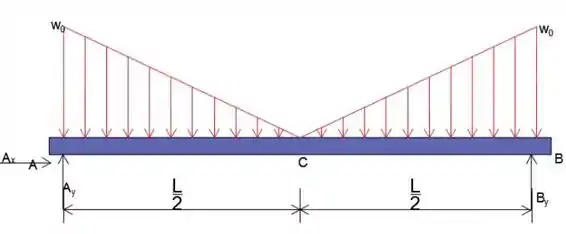
Passo 3

Agora, vamos considerar o momento de condição de equilíbrio sobre A

∑ M A = 0

R B ⋅ l A C - w 0 l A C 2 ⋅ l A C 3 - w 0 l C B 2 ⋅ l A C + 2 l C B 3 = 0 R B ⋅ L - w 0 ⋅ L 2 24 - 5 w 0 ⋅ L 2 24 = 0 R B = w 0 ⋅ L 4

Agora, vamos considerar a força vertical de equilíbrio

∑ F y = 0

R A + R B - w 0 l A C 2 - w 0 l C B 2 = 0 R A + w 0 ⋅ L 2 4 - w 0 ⋅ L 2 4 - w 0 ⋅ L 2 4 = 0 R B = w 0 ⋅ L 4

Passo 4

Diagrama da força de cisalhamento

V A = R A = w 0 ⋅ L 4 força em A

V C = R A - w 0 l A C 2 =0 força em C

V B = R A - w 0 l A C 2 - w 0 l C B 2 = - w 0 ⋅ L 4 k N força em B

Passo 5

Diagrama da Força de cisalhamento

M A = 0 momento de flexão em A

momento de flexão em C

M C = R B ⋅ l A C - w 0 l A C 2 ⋅ l A C 3 = w 0 L 2 24

momento de flexão em B

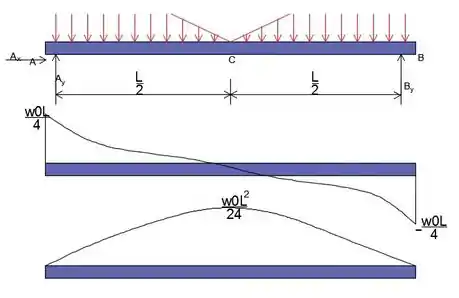
M B = R A ⋅ l A B - w 0 l A C 2 ⋅ l A C 3 - w 0 l C B 2 ⋅ l A C + 2 l C B 3 = w 0 L 4 ⋅ L - w 0 ⋅ L 2 24 - 5 w 0 ⋅ L 2 24 = 0 k N m

O momento fletor máximo é colocado onde a força de cisalhamento é zero.

M m a x = M C = w 0 L 2 24

Resposta

M m a x = w 0 L 2 24

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o volume V gerado girando a área elíptica em 180 ° em torno do eixo z.
Usando os métodos deste artigo, determine a área de superfície A e o volume V do corpo formado girando a área retangular em 360 em torno do eixo z.
Determine a coordenada y do centróide da área sombreada. (Dica: consulte a solução do Problema 5/41.)
Determine as coordenadas do centro de massa do suporte, que é construído a partir de uma chapa de espessura uniforme.
O tanque de armazenamento de água é uma concha de revolução e deve ser pulverizado com duas camadas de tinta que tem uma cobertura de 500 pés2 por galão. O engenheiro (que se lembra da mecânica) consu