Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 140

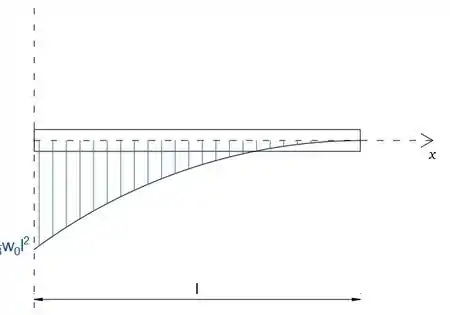
Desenhe os diagramas de cisalhamento e momento para a viga cantilever carregada linearmente e especifique o momento fletor MA no suporte A

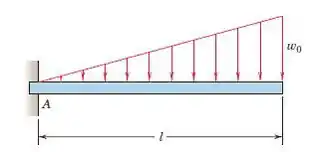
Passo 1

Primeiro, vamos determinar as forças de reação do diagrama de corpo livre usando as equações de equilíbrio

Observe que substituímos as cargas distribuídas por suas resultantes

R = 1 2 w 0 l

∑ M A = 0

R ⋅ 2 l 3 - M A = 0 M A = R ⋅ 2 l 3 M A = 1 2 w 0 l ⋅ 2 l 3 M A = 1 3 w 0 l 2

∑ F x = 0

X A = 0

∑ F y = 0

R - Y A = 0 Y A = R Y A = 1 2 w 0 l

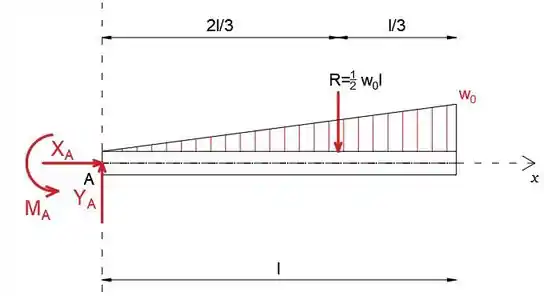
Passo 2

A partir daqui, podemos construir o diagrama de força cortante

Usando a fórmula V x = V x - 1 + Δ V , calcularemos as forças de cisalhamento da esquerda para a direita

V x = 0 = Y A = 1 2 w 0 l V x = l = 1 2 w 0 l - 1 2 w 0 l = 0

Observe que o diagrama de força cortante é uma curva, por causa da carga triangular distribuída e a inclinação está aumentando do ponto A até o final da viga, uma vez que a carga está aumentando na mesma faixa.

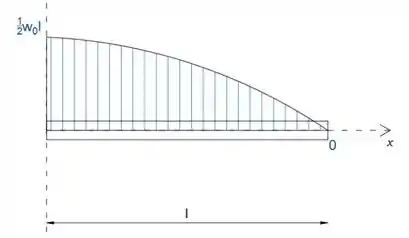
Passo 3

Observe que o momento máximo está em A (momento negativo), após o qual o diagrama de momento aumenta e a inclinação diminui com o comprimento, pois o diagrama da força cortante diminui com o comprimento.

M A = - 1 3 w 0 l 2

Resposta

M A = - 1 3 w 0 l 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a massa do comprimento de um quarto de círculo da mangueira do radiador. O diâmetro interno é 40 mm, a espessura da parede é 4 mm e a densidade do material de borracha é 1050 kg / m3.
A área de um quarto circular é girada 360 ° em torno do eixo y. Determine o volume do corpo resultante, que é uma parte de uma esfera.
O corpo mostrado em seção transversal é um anel circular completo formado pela rotação da área octogonal em torno do eixo z. Toda a superfície deve ser coberta com um revestimento especial. Determine
O abajur mostrado é construído em aço de 0,6 mm de espessura e é simétrico em relação ao eixo z. Ambas as extremidades superior e inferior estão abertas. Determine a massa do abajur. Considere os raio
O arco circular é girado 360 ° em torno do eixo y. Determine a área da superfície externa S do corpo resultante, que é uma parte de uma casca esférica.