Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Rao - Vibrações mecânicas- Ed: 4º - Capítulo 8.Problemas - Ex. 37

37. Um viga uniforme fixa-fixa de comprimento 2 l é simplesmente apoiada em seu ponto médio. Deduza a equação de frequência para a vibração transversal da viga.

Passo 1

E aí, galerinha!

Simbora lá, meus queridos!

Bom, rapaziada e moças! Vamo começar fazendo um esboço dessa viga, pra entender melhor o que a gente tem que fazer...

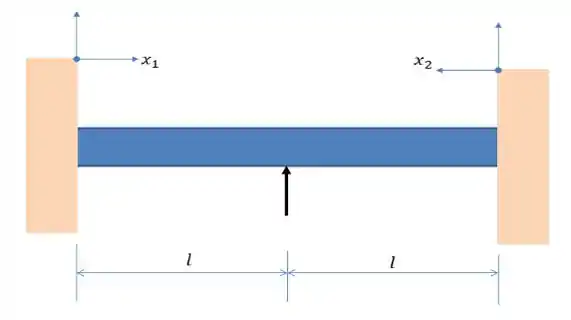
Passo 2

Agora, como a viga é fixa-fixa, vamos dar uma olhada na figura abaixo pra ver qual equação a gente vai usar...

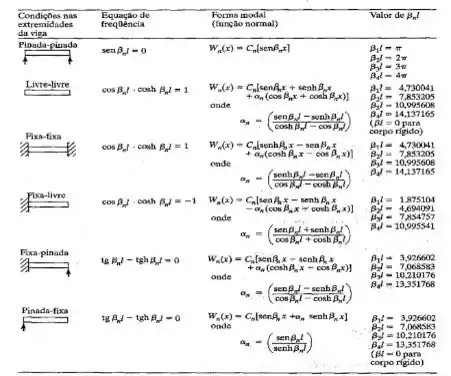
Temos então, que baseado na primeira coordenada x 1 que definimos como...

W 1 x 1 = C 1 cos ⁡ β x 1 + C 2 sen ⁡ β x 1 + C 3 cosh ⁡ β x 1 + C 4 senh ⁡ β x 1

Tirando a derivada em relação à x 1 :

d W 1 x 1 d x 1 = - C 1 β sen ⁡ β x 1 + C 2 β cos ⁡ β x 1 + C 3 β senh ⁡ β x 1 + C 4 β cosh ⁡ β x 1

Como a nossa viga está fixa em...

x 1 = 0

Então, temos que...

W 1 0 = 0

d W 1 0 d x 1 = 0

Substituindo assim, x 1 = 0 :

W 1 x 1 = C 1 cos ⁡ β x 1 + C 2 sen ⁡ β x 1 + C 3 cosh ⁡ β x 1 + C 4 senh ⁡ β x 1

C 1 cos ⁡ 0 + C 2 sen ⁡ 0 + C 3 cosh ⁡ 0 + C 4 senh ⁡ 0 = 0

C 1 + C 3 = 0

C 1 = - C 3

d W 1 x 1 d x 1 = - C 1 β sen ⁡ β x 1 + C 2 β cos ⁡ β x 1 + C 3 β senh ⁡ β x 1 + C 4 β cosh ⁡ β x 1

- C 1 β sen ⁡ 0 + C 2 β cos ⁡ 0 + C 3 β senh ⁡ 0 + C 4 β cosh ⁡ 0 = 0

C 2 + C 4 = 0

C 2 = - C 4

Substituindo essas relações na equação de movimento que temos...

W 1 x 1 = C 1 cos ⁡ β x 1 + C 2 sen ⁡ β x 1 + C 3 cosh ⁡ β x 1 + C 4 senh ⁡ β x 1

W 1 x 1 = - C 3 cos ⁡ β x 1 - C 4 sen ⁡ β x 1 + C 3 cosh ⁡ β x 1 + C 4 senh ⁡ β x 1

W 1 x 1 = C 3 cosh ⁡ β x 1 - cos ⁡ β x 1 + C 4 ( senh ⁡ β x 1 - sen ⁡ β x 1 )

Passo 3

Uma vez que a viga está simplesmente apoiada em seu ponto médio, também temos que...

W 1 l = 0

Assim, ficamos com...

W 1 x 1 = C 3 cosh ⁡ β x 1 - cos ⁡ β x 1 + C 4 ( senh ⁡ β x 1 - C 4 sen ⁡ β x 1 )

C 3 cosh ⁡ β l - cos ⁡ β l + C 4 senh ⁡ β l - sen ⁡ β l = 0

C 3 = - C 4 senh ⁡ β l - C 4 sen ⁡ β l cosh ⁡ β l - cos ⁡ β l

E usando essa relação, vamos substituir novamente na equação de W 1 ( x 1 ) :

W 1 x 1 = C 3 cosh ⁡ β x 1 - cos ⁡ β x 1 + C 4 ( senh ⁡ β x 1 - sen ⁡ β x 1 )

W 1 x 1 = - C 4 senh ⁡ β l - C 4 sen ⁡ β l cosh ⁡ β l - cos ⁡ β l cosh ⁡ β x 1 - cos ⁡ β x 1 + C 4 ( senh ⁡ β x 1 - sen ⁡ β x 1 )

W 1 x 1 = C 4 ( senh ⁡ β x 1 - sen ⁡ β x 1 ) + senh ⁡ β l - C 4 sen ⁡ β l cosh ⁡ β l - cos ⁡ β l cosh ⁡ β x 1 - cos ⁡ β x 1

Ficamos então, com a seguinte equação acima!

Resposta

W 1 x 1 = C 4 ( senh ⁡ β x 1 - sen ⁡ β x 1 ) + senh ⁡ β l - C 4 sen ⁡ β l cosh ⁡ β l - cos ⁡ β l cosh ⁡ β x 1 - cos ⁡ β x 1

Ver Outros Exercícios desse livro