Envoltória
Teoria
Introdução
Até aqui vimos como calculamos para uma seção, a pior situação em que ela pode estar submetida.
Vimos que para fazer isso precisamos de duas coisas.
A primeira é a linha de influência, que nos permite saber o momento, ou cortante, ou o que for pedido, em uma determinada seção, quando andamos com uma carga unitária por toda a viga.
A segunda, vimo na aula de conceito, precisamos de um carregamento que multiplicaremos pela maior ordenada da nossa linha de influência, caso seja uma carga concentrada, ou pela área, caso seja uma carga distribuída.
Esses dois conceitos juntos, nos darão a pior situação naquela seção que pedimos.
Agora pensa no seguinte, e se eu juntasse todas as piores situações de várias seções diferentes, o que isso me daria?
Envoltória
Ai que entra o novo conceito, que é calcular a envoltória. Em resumo, a envoltória é o conjunto dos piores valores que a nossa viga estará submetida para cada uma das seções, levando em consideração posicionar o carregamento sempre na pior posição da linha de influência de cada seção.
Parece meio embolado, certo? Mas vamos fazer um exemplo bem completo para ficarmos craques nesse tipo de questão, vamos ao passo a passo?
A viga que usaremos será
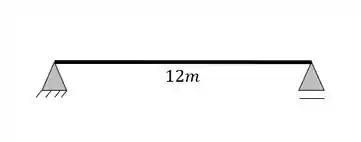
E as cargas que usaremos serão de dois tipos
Permanente: Nunca muda
Variável: Podemos mudar a carga concentrada e distribuída de acordo com a linha de influência, respeitando a distância entre as cargas concentradas.
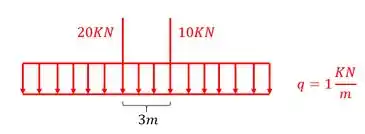
E o nosso objetivo é determinar a envoltória de momento fletor. Lembrando que qualquer outra envoltória (cortante, Reação de apoio, Balanço) seguirá mesmo passo a passo mostrado abaixo.
Passo 1: Definir as seções chaves
A primeira coisa é, não temos como calcular tudo para todas as seções, até porque seriam milhares de seções, por isso, iremos calcular apenas para algumas seções chaves, e a partir delas calcularemos a nossa envoltória. As nossas seções chaves serão
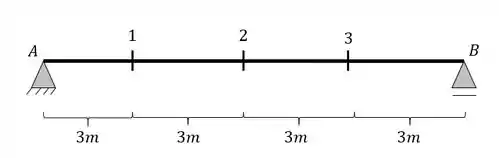
Foram definidas arbitrariamente, apenas pois serão mais fáceis de calcular, mas você pode escolher a seção que quiser.
Passo 2: Calcular a linha de influência de cada uma das seções
Agora vamos fazer exatamente o que aprendemos nas aulas anteriores a essa, vamos usar os nossos conhecimentos de linha de influência para determinarmos as linhas de influencias de cada uma das seções, nesse caso, usarei o método gráfico que aprendemos na aula de linha de influência de momentos e cortantes pelo método gráfico para calcularmos cada linha de influência.
- Para a seção A
- Para a seção 1
- Para a seção 2
- Para a seção 3
- Para a seção B
- Para a seção A
- Para a seção 1
- Para a seção 2
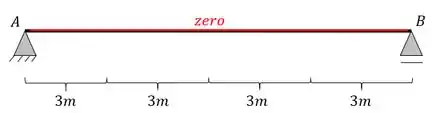
A linha de influência da seção A, será o momento fletor na seção A conforme andamos com uma carga unitária sobre toda a Barra, nesse caso, o momento será zero, logo a nossa linha de influência será
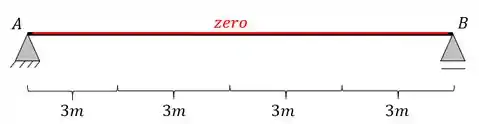
A linha de influência da seção 1 será feita pelo método gráfico, e dessa forma teremos
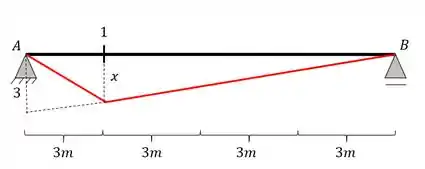
Fazendo a regra de 3 teremos
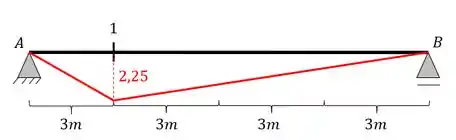
A linha de influência da seção 2 será feita pelo método gráfico, e dessa forma teremos o mesmo esquema feito acima, porém com valores diferentes
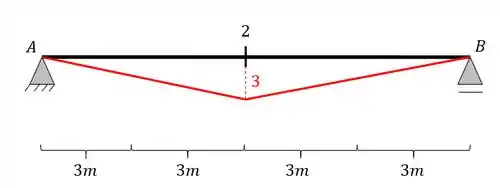
A linha de influência da seção 3 será feita pelo método gráfico, e dessa forma teremos o mesmo esquema feito acima, porém com valores diferentes
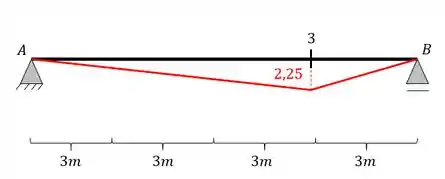
A linha de influência da seção B, será o momento fletor na seção B conforme andamos com uma carga unitária sobre toda a Barra, nesse caso, o momento será zero, logo a nossa linha de influência será
Passo 3: Calcular o valor do pior momento em cada seção com a carga variável
Agora entra o que aprendemos na aula de conceito de Linha de influência, devemos posicionar o carregamento de forma a ter o maior valor de momento, vamos fazer esse calculo para cada uma das seções
Como o diagrama da seção A é zero, independente da posição que você coloque o carregamento, o momento lá será zero, então teremos que
Como temos simetria, esses valores de momentos serão idênticos na seção B, ou seja, calculando a seção A já conseguimos calcular a seção B, que é exatamente igual.
Nesse caso sempre colocaremos a maior carga concentrada na maior ordenada, e a segunda carga concentrada, sempre do lado com menor declividade, dessa forma, teremos
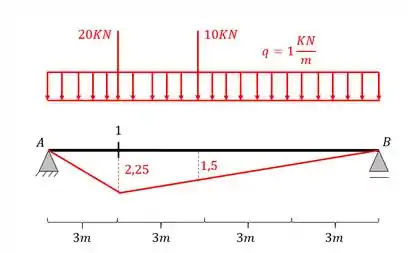
Lembrando que a ordenada de 1,5, foi calculada também por regra de 3, ou seja, vc consegue a ordenada que quiser a partir da linha de influência, usando apenas regra de 3.
Pra carga concentrada basta apenas multiplicar a ordenada pelo carregamento
Pra carga distribuída basta multiplicar a carga pela área que ela pega, nesse caso teremos
Dessa forma teremos que o será
Obs:. Vale lembrar que devemos calcular tanto o momento máximo positivo, quanto o momento máximo negativo, porém, como nesse caso a nossa linha de influência só tem momento positivo, iremos colocar que o momento máximo negativo devido a carga variável é zero.
Como temos simetria, esses valores de momentos serão idênticos na seção 3, ou seja, calculando a seção 1 já conseguimos calcular a seção 3, que é exatamente igual.
Nesse caso ambas as declividades serão iguais, bastando escolher apenas um dos lados para colocar a segunda carga concentrada, com isso teremos
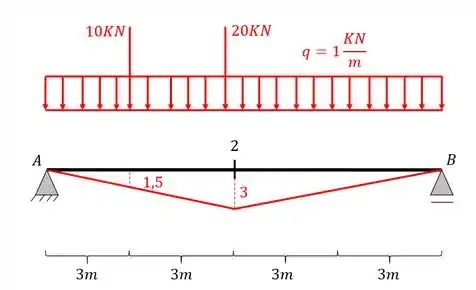
Lembrando que a ordenada de 1,5, foi calculada também por regra de 3, ou seja, vc consegue a ordenada que quiser a partir da linha de influência, usando apenas regra de 3.
Pra carga concentrada basta apenas multiplicar a ordenada pelo carregamento
Pra carga distribuída basta multiplicar a carga pela área que ela pega, nesse caso teremos
Dessa forma teremos que o será
Obs:. Vale lembrar que devemos calcular tanto o momento máximo positivo, quanto o momento máximo negativo, porém, como nesse caso a nossa linha de influência só tem momento positivo, iremos colocar que o momento máximo negativo devido a carga variável é zero.
Passo 4: Calcular os momentos devido a carga permanente
Nesse caso é bem simples, como a carga permanente é fixa, basta calcularmos o diagrama de momento fletor e ver qual o valor do momento em cada seção, como estamos falando de diagrama de momento fletor, basta ir na aula de esforços internos em vigas, no assunto flexão, ou na ala de vigas simples, no assunto vigas. Então o nosso diagrama de momentos, com os momentos de cada seção, será.
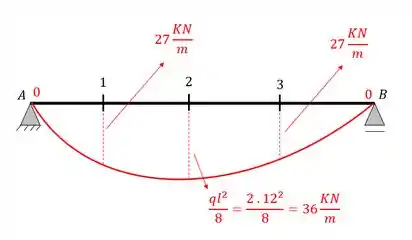
Obs:. Tomar muito cuidado, aqui nós calculamos o momento fletor direto pois estamos falando de uma carga permanente que não se move e sempre dará valores fixos pra seção, no caso da carga variável, nós calculamos linhas de influências para saber onde seria a pior posição para colocarmos a nossa carga variável, sempre lembre disso, é muito importante entender que
Passo 5: Fazer a tabela e desenhar a Envoltória
A tabela que devemos fazer é
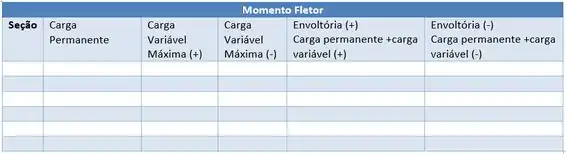
Perceba que a carga permanente é fixa, temos o espaço da carga móvel máxima positiva e negativa, e aí entram os valores das envoltórias
Perceba que independente do sinal a carga permanente é sempre a mesma, mas a carga variável deve ser obrigatoriamente positiva. Da mesma forma.
Completando a nossa tabela com os nossos valores teremos.
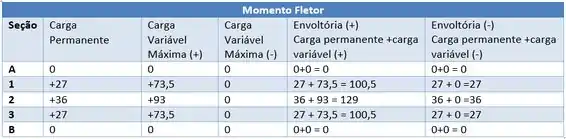
Com a nossa tabela de valores conseguimos desenhar a nossa Envoltória, basta pegarmos cada um dos valores encontrados e coloca-los na nossa viga
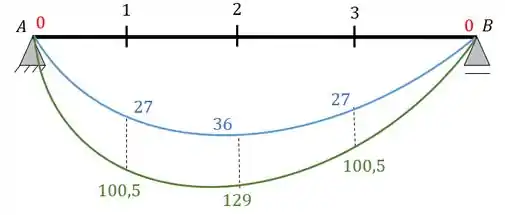
E essa é a nossa envoltória, perceba como ela é importante, pois ela indica o seguinte.
O mínimo valor de momento ao qual a nossa seção está sujeita é marcado pela linha azul, ou seja, sempre terá algum momento nas nossas seções, e o mínimo que eles atingem é a curva azul.
O máximo valor de momento ao qual a nossa seção está sujeita é marcado em verde, ou seja, a nossa seção não sofre momentos infinitos, o máximo que eles podem atingir, em cada seção, sendo a pior situação daquela seção para as cargas dadas, está marcado pelo limite da curva verde.
Esse é o principal objetivo da nossa envoltória, nos permitir ver os limites de carregamento ao qual a nossa estrutura está sujeita.
Agora chega de falar e vamos treinar, pronto para fazer os exercícios?
Vamos lá treinar, para ficarmos craques em Envoltória e tirar aquele 10 redondo.
Envoltória
Passo 1: Definir as seções chaves
Passo 2: Calcular a linha de influência de cada uma das seções
Passo 3: Calcular o valor do pior momento em cada seção com a carga variável
Passo 4: Calcular os momentos devido a carga permanente
Passo 5: Fazer a tabela e desenhar a Envoltória
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Abaixo é dado uma viga com suas seções usadas para Cálculo, assim como a sua tabela com máximos e mínimos de Cortantes por seção. Usando seus conhecimentos de envoltória, determine os máximos e mínimos de cada seção e desenhe a Envoltória de Cortantes dessa viga de acordo com os carregamentos dados abaixo.
Passo 1
Como já sabemos sempre temos uma ordem de solução para o nosso problema, no caso de envoltórias o nosso passo a passo é o seguinte.
- Primeiro nós pegamos a nossa viga e separamos ela em várias seções que facilitaram o nosso cálculo.
- Em seguida, para cada uma das seções desenhamos a sua linha de influência, que pode ser de cortantes, momentos fletores, ou reação de apoio.
- Tendo em mãos as linhas de influências e os trem-tipos posicionamos para cada linha de influência, de cada uma das seções podemos determinar quais serão os máximos e os mínimos de cada uma das seções devido a carga móvel. OBS: é muito importante lembrar que faremos esses máximos e mínimos para cada uma das seções, ou seja, usamos a linha de influência de cada seção, e pra todas elas posicionamos o trem tipo de forma a dar a pior situação positiva e a pior situação negativa devido a carga móvel.
- A carga permanente é a mais fácil, pois basta colocarmos ela espalhada por toda a viga e calcular normalmente os esforços que ela causa em cada seção, seja ele negativo ou positivo, pois vale lembrar que a carga permanente, como o próprio nome diz, é permanente, então independente da carga móvel, ela sempre irá causar esforços permanentes na viga, e são exatamente esses esforços que iremos calcular.
- Depois montaremos a nossa tabela de máximos e mínimos, e com ela faremos as devidas combinações de carga móvel e permanente a fim de calcularmos os valores da nossa envoltória.
- Por fim, com os valores da nossa envoltória, podemos montar o diagrama referente a nossa envoltória, e com ele completar todo o nosso passo a passo do problema.
Perceba que no nosso problema já foi executado até o passo 4, faltando apenas os dois últimos passos, que são exatamente os passos 5 e 6. Dessa forma vamos por as mãos a obra.
Passo 2
Como dito anteriormente, já fizemos até o passo 4 do nosso problema, o passo 5 consiste em exatamente fazermos a combinação do que ocorre devido a carga permanente, com o que ocorre devido a carga móvel, para isso faremos o seguinte
Assim calculamos o máximo valor positivo de cortante que pode ocorrer na seção A da nossa viga, se quisermos saber o máximo valor negativo de cortante que pode ocorrer na seção A fazemos a mesma combinação, mas combinando a carga permanente com a possibilidade negativa, dessa forma teremos que
Fazendo isso em todas as seções teremos os seguintes valores para a nossa envoltória.
E assim finalizamos o quinto passo.
Passo 3
Finalizado o quinto passo vemos que falta apenas o último passo que consiste em desenharmos a nossa envoltória na nossa viga, para isso vamos definir primeiro a direção dos sinais. No caso de envoltória a nossa ordem de sinais fica
Fazendo isso, podemos marcar na nossa viga. Para cada uma das seções, os valores que encontramos na nossa envoltória, com isso teremos
Primeiro marcamos toda a parte positiva da nossa envoltória, que foi definida no lado esquerdo da nossa tabela na parte de envoltória, vamos definir tudo aquilo que encontramos do lado direito da nossa tabela
Juntado os dois gráficos teremos que a nossa envoltória será
Resposta
Envoltória de cortantes com seus valores máximos e mínimos
Exercício Resolvido #2
Elaboração Própria
Abaixo é dado uma viga com suas seções usadas para Cálculo, assim como a sua tabela com máximos e mínimos de Cortantes por seção. Usando seus conhecimentos de envoltória, determine os máximos e mínimos de cada seção e desenhe a Envoltória de Cortantes dessa viga de acordo com os carregamentos dados abaixo.
Passo 1
Como já sabemos sempre temos uma ordem de solução para o nosso problema, no caso de envoltórias o nosso passo a passo é o seguinte.
- Primeiro nós pegamos a nossa viga e separamos ela em várias seções que facilitaram o nosso cálculo.
- Em seguida, para cada uma das seções desenhamos a sua linha de influência, que pode ser de cortantes, momentos fletores, ou reação de apoio.
- Tendo em mãos as linhas de influências e os trem-tipos posicionamos para cada linha de influência, de cada uma das seções podemos determinar quais serão os máximos e os mínimos de cada uma das seções devido a carga móvel. OBS: é muito importante lembrar que faremos esses máximos e mínimos para cada uma das seções, ou seja, usamos a linha de influência de cada seção, e pra todas elas posicionamos o trem tipo de forma a dar a pior situação positiva e a pior situação negativa devido a carga móvel.
- A carga permanente é a mais fácil, pois basta colocarmos ela espalhada por toda a viga e calcular normalmente os esforços que ela causa em cada seção, seja ele negativo ou positivo, pois vale lembrar que a carga permanente, como o próprio nome diz, é permanente, então independente da carga móvel, ela sempre irá causar esforços permanentes na viga, e são exatamente esses esforços que iremos calcular.
- Depois montaremos a nossa tabela de máximos e mínimos, e com ela faremos as devidas combinações de carga móvel e permanente a fim de calcularmos os valores da nossa envoltória.
- Por fim, com os valores da nossa envoltória, podemos montar o diagrama referente a nossa envoltória, e com ele completar todo o nosso passo a passo do problema.
Perceba que no nosso problema já foi executado até o passo 4, faltando apenas os dois últimos passos, que são exatamente os passos 5 e 6. Dessa forma vamos por as mãos a obra.
Passo 2
Como dito anteriormente, já fizemos até o passo 4 do nosso problema, o passo 5 consiste em exatamente fazermos a combinação do que ocorre devido a carga permanente, com o que ocorre devido a carga móvel, para isso faremos o seguinte
Assim calculamos o máximo valor positivo de cortante que pode ocorrer na seção A da nossa viga, se quisermos saber o máximo valor negativo de cortante que pode ocorrer na seção A fazemos a mesma combinação, mas combinando a carga permanente com a possibilidade negativa, dessa forma teremos que
Fazendo isso em todas as seções teremos os seguintes valores para a nossa envoltória.
E assim finalizamos o quinto passo.
Passo 3
Finalizado o quinto passo vemos que falta apenas o último passo que consiste em desenharmos a nossa envoltória na nossa viga, para isso vamos definir primeiro a direção dos sinais. No caso de envoltória a nossa ordem de sinais fica
Fazendo isso, podemos marcar na nossa viga. Para cada uma das seções, os valores que encontramos na nossa envoltória, com isso teremos
Primeiro marcamos toda a parte positiva da nossa envoltória, que foi definida no lado esquerdo da nossa tabela na parte de envoltória, vamos definir tudo aquilo que encontramos do lado direito da nossa tabela
Juntado os dois gráficos teremos que a nossa envoltória será
Resposta
Envoltória de cortantes com seus valores máximos e mínimos
Exercício Resolvido #3
Elaboração Própria
Abaixo é dado uma viga com suas seções usadas para Cálculo, assim como a sua tabela com máximos e mínimos de momentos fletores por seção. Usando seus conhecimentos de envoltória, determine os máximos e mínimos de cada seção e desenhe a Envoltória de momentos dessa viga de acordo com os carregamentos dados abaixo.
Passo 1
Como já sabemos sempre temos uma ordem de solução para o nosso problema, no caso de envoltórias o nosso passo a passo é o seguinte.
- Primeiro nós pegamos a nossa viga e separamos ela em várias seções que facilitaram o nosso cálculo.
- Em seguida, para cada uma das seções desenhamos a sua linha de influência, que pode ser de cortantes, momentos fletores, ou reação de apoio.
- Tendo em mãos as linhas de influências e os trem-tipos posicionamos para cada linha de influência, de cada uma das seções podemos determinar quais serão os máximos e os mínimos de cada uma das seções devido a carga móvel. OBS: é muito importante lembrar que faremos esses máximos e mínimos para cada uma das seções, ou seja, usamos a linha de influência de cada seção, e pra todas elas posicionamos o trem tipo de forma a dar a pior situação positiva e a pior situação negativa devido a carga móvel.
- A carga permanente é a mais fácil, pois basta colocarmos ela espalhada por toda a viga e calcular normalmente os esforços que ela causa em cada seção, seja ele negativo ou positivo, pois vale lembrar que a carga permanente, como o próprio nome diz, é permanente, então independente da carga móvel, ela sempre irá causar esforços permanentes na viga, e são exatamente esses esforços que iremos calcular.
- Depois montaremos a nossa tabela de máximos e mínimos, e com ela faremos as devidas combinações de carga móvel e permanente a fim de calcularmos os valores da nossa envoltória.
- Por fim, com os valores da nossa envoltória, podemos montar o diagrama referente a nossa envoltória, e com ele completar todo o nosso passo a passo do problema.
Perceba que no nosso problema já foi executado até o passo 4, faltando apenas os dois últimos passos, que são exatamente os passos 5 e 6. Dessa forma vamos por as mãos a obra.
Passo 2
Como dito anteriormente, já fizemos até o passo 4 do nosso problema, o passo 5 consiste em exatamente fazermos a combinação do que ocorre devido a carga permanente, com o que ocorre devido a carga móvel, para isso faremos o seguinte
Assim calculamos o máximo valor positivo de cortante que pode ocorrer na seção A da nossa viga, se quisermos saber o máximo valor negativo de cortante que pode ocorrer na seção A fazemos a mesma combinação, mas combinando a carga permanente com a possibilidade negativa, dessa forma teremos que
Fazendo isso em todas as seções teremos os seguintes valores para a nossa envoltória.
E assim finalizamos o quinto passo.
Passo 3
Finalizado o quinto passo vemos que falta apenas o último passo que consiste em desenharmos a nossa envoltória na nossa viga, para isso vamos definir primeiro a direção dos sinais. No caso de envoltória a nossa ordem de sinais fica
Fazendo isso, podemos marcar na nossa viga. Para cada uma das seções, os valores que encontramos na nossa envoltória, com isso teremos
Primeiro marcamos toda a parte positiva da nossa envoltória, que foi definida no lado esquerdo da nossa tabela na parte de envoltória, vamos definir tudo aquilo que encontramos do lado direito da nossa tabela
Juntado os dois gráficos teremos que a nossa envoltória será
Resposta
Envoltória de momentos com seus valores máximos e mínimos
Exercício Resolvido #4
HYPERLINK "https://www.youtube.com/watch?v=quiqLT88ycg" https://www.youtube.com/watch?v=quiqLT88ycg
Abaixo é dado uma viga com suas seções usadas para Cálculo, assim como a sua tabela com máximos e mínimos de momentos fletores por seção. Usando seus conhecimentos de envoltória, determine os máximos e mínimos de cada seção e desenhe a Envoltória de momentos dessa viga de acordo com os carregamentos dados abaixo.
Passo 1
Como já sabemos sempre temos uma ordem de solução para o nosso problema, no caso de envoltórias o nosso passo a passo é o seguinte.
- Primeiro nós pegamos a nossa viga e separamos ela em várias seções que facilitaram o nosso cálculo.
- Em seguida, para cada uma das seções desenhamos a sua linha de influência, que pode ser de cortantes, momentos fletores, ou reação de apoio.
- Tendo em mãos as linhas de influências e os trem-tipos posicionamos para cada linha de influência, de cada uma das seções podemos determinar quais serão os máximos e os mínimos de cada uma das seções devido a carga móvel. OBS: é muito importante lembrar que faremos esses máximos e mínimos para cada uma das seções, ou seja, usamos a linha de influência de cada seção, e pra todas elas posicionamos o trem tipo de forma a dar a pior situação positiva e a pior situação negativa devido a carga móvel.
- A carga permanente é a mais fácil, pois basta colocarmos ela espalhada por toda a viga e calcular normalmente os esforços que ela causa em cada seção, seja ele negativo ou positivo, pois vale lembrar que a carga permanente, como o próprio nome diz, é permanente, então independente da carga móvel, ela sempre irá causar esforços permanentes na viga, e são exatamente esses esforços que iremos calcular.
- Depois montaremos a nossa tabela de máximos e mínimos, e com ela faremos as devidas combinações de carga móvel e permanente a fim de calcularmos os valores da nossa envoltória.
- Por fim, com os valores da nossa envoltória, podemos montar o diagrama referente a nossa envoltória, e com ele completar todo o nosso passo a passo do problema.
Perceba que no nosso problema já foi executado até o passo 4, faltando apenas os dois últimos passos, que são exatamente os passos 5 e 6. Dessa forma vamos por as mãos a obra.
Passo 2
Como dito anteriormente, já fizemos até o passo 4 do nosso problema, o passo 5 consiste em exatamente fazermos a combinação do que ocorre devido a carga permanente, com o que ocorre devido a carga móvel, para isso faremos o seguinte
Assim calculamos o máximo valor positivo de cortante que pode ocorrer na seção A da nossa viga, se quisermos saber o máximo valor negativo de cortante que pode ocorrer na seção A fazemos a mesma combinação, mas combinando a carga permanente com a possibilidade negativa, dessa forma teremos que
Fazendo isso em todas as seções teremos os seguintes valores para a nossa envoltória.
E assim finalizamos o quinto passo.
Passo 3
Finalizado o quinto passo vemos que falta apenas o último passo que consiste em desenharmos a nossa envoltória na nossa viga, para isso vamos definir primeiro a direção dos sinais. No caso de envoltória a nossa ordem de sinais fica
Fazendo isso, podemos marcar na nossa viga. Para cada uma das seções, os valores que encontramos na nossa envoltória, com isso teremos
Primeiro marcamos toda a parte positiva da nossa envoltória, que foi definida no lado esquerdo da nossa tabela na parte de envoltória, vamos definir tudo aquilo que encontramos do lado direito da nossa tabela
Juntado os dois gráficos teremos que a nossa envoltória será
Resposta
Envoltória de momentos com seus valores máximos e mínimos
