Linha de Influencia Vigas com Rótulas internas e Vigas Gerber
Produzido por Pablo RicardoTeoria
Introdução
Uma coisa que precisamos entender é que sempre que o assunto for Linha de influência, o conceito sempre será o mesmo, precisamos andar com uma carga unitária por toda a viga e ir anotando os valores para uma determinada seção, conforme andamos por toda a viga com a carga unitária.
Mas na viga Gerber e com Rótula interna tem alguns macetes que precisamos conhecer para não errarmos bobeira, esses macetes serão os métodos gráficos para cada uma dessas vigas, tomando sempre os cuidados devidos para não errarmos bobeira, vamos entender o que temos que fazer então? Vamos lá !!!!
Método Gráfico de momento fletor em vigas com rótula interna
Nesse caso, um exemplo de viga com rótula interna é

Imagine que queremos analisar a linha de influência de momento fletor para a seguinte seção

Agora veja o seguinte, se não houvesse as rótulas e os apoios externos, saberíamos determinar facilmente a nossa linha de influência, já que seria simplesmente uma viga biapoiada com balanço, com isso teríamos a seguinte linha de influência

Como as rótulas e os apoios afetariam a nossa linha de influência?
Veja que pelo conceito de linha de influência se colocarmos uma carga unitária no apoio extremo, ele transferira toda a carga para o apoio, ou seja, não haverá momento fletor na seção A.

Agora pensa no seguinte, se as linhas de influências em estruturas isostáticas sempre são retas, e sabemos que no ultimo apoio é zero, basta ligarmos o final da nossa linha de influência no apoio, e com isso teremos

E essa será a nossa linha de influência para momentos fletores.
Método Gráfico de Cortante em vigas com rótula interna
Da mesma forma que o momento, se desprezássemos a rótula e o apoio extremos, já saberíamos desenhar a nossa linha de influência para cortante, que seria

Agora pense novamente pelo conceito de linha de influência, se fosse colocado uma carga unitária no apoio extremo, qual seria o cortante na seção A?
Exatamente, como a carga seria toda passada para o apoio, não interferiria no resto da estrutura, logo o cortante quando colocamos a carga unitária nas extremidades é zero, e como linha de influência são retas, basta ligar o final da linha de influência no apoio, com isso a nossa linha de Influência passa a ser

Método Gráfico de Reação de apoio em vigas com rótula interna
Vamos continuar com o pensamento anterior vamos desprezar a rótula e o apoio extremo, já saberíamos desenhar a nossa linha de influência para Reação de apoio, que seria
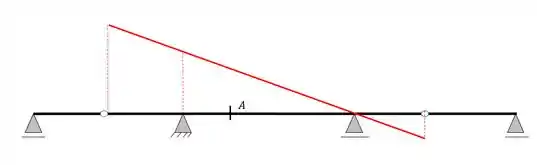
E se usarmos o conceito, de novo, colocando a carga unitária na extremidade, teremos
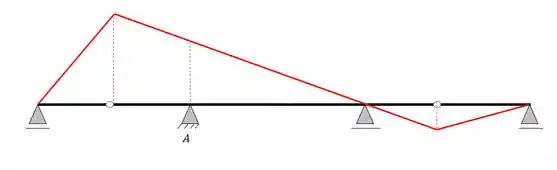
E essa é a linha de influência da reação de apoio A.
Método Gráfico de Momento e cortante no Balanço antes da Rótula em vigas com rótula interna
E se o professor pedir a linha de influência de momento e de cortante no balanço?
Usamos o mesmo conceito, finge que não existe a rótula e o apoio externo, e com isso sabemos que as linhas de influencias são
Para o momento fletor

Para o cortante

Agora usando exatamente o mesmo conceito anterior, basta ligar o final da linha de influência no nosso apoio, e teremos
Para o momento

Para o cortante

E perceba que quando estamos no balanço, apenas o balanço é afetado, isso ocorre pois se colocarmos a carga unitária em qualquer outro ponto da nossa viga, em nada afetará a nossa seção no Balanço.
Método Gráfico de Momento e cortante no Balanço Depois da Rótula em vigas com rótula interna
E se colocarmos a seção depois da rótula?
Ai vale usar o conceito que vimos na aula de Viga Gerber no assunto vigas, porque pensa só, podemos quebrar essa viga na rótula e separar ela do resto da estrutura, e com isso teremos uma viga biapoiada, que já sabemos como fazer qualquer diagrama nela, e pensa só, se ela tá separada do resto da estrutura, posso por cargas unitárias em todo o resto da estrutura que em nada irá afetar a nossa viga biapoiada, vamos ver um desenho para nos ajudar a visualizar
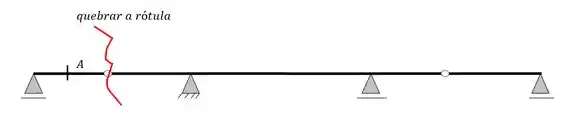
Separando a viga da esquerda e colocando um apoio fictício, teremos

Agora é simples, quais as linhas de influência da viga Biapoiada?
Para o momento

Para o cortante

E perceba, todo o resto da viga permanece inalterado.
Método Gráfico de momento fletor em vigas Gerber
O método gráfico para viga Gerber segue a mesma sequencia de passos da viga com rótula interna, basta vermos a região com o trecho Gerber como estávamos vendo o trecho da rótula com apoios extremos nas vigas com rótula interna, ou seja, em um primeiro momento ignoramos completamente a existência do trecho, e depois fechamos os trechos que faltam. Vamos então usar a seguinte viga Gerber

Veja que o apoio extremo da esquerda, assim com a sua rótula podem ser ignorados, ou seja, se fizéssemos a linha de influência do trecho que conhecemos, teríamos

Agora pensa no seguinte, nas vigas Gerber podemos sempre separar o trecho do meio, da seguinte maneira
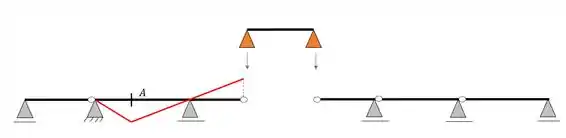
Perceba que se colocarmos cargas unitárias no trecho Gerber separado, ele transferirá carga para a nossa viga com a seção A, ou seja, toda carga unitária no trecho Gerber afeta nossa seção. Mas e se colocarmos a carga unitária aqui
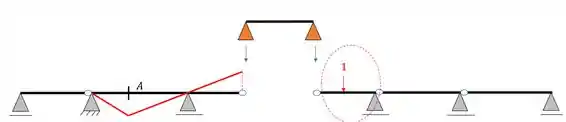
Perceba que em nada ela afetará a nossa seção, ou seja, toda aquela região terá linha de influência igual a zero, com isso basta ligar o fim da nossa linha de influência na nossa rótula final do trecho Gerber

Método Gráfico de Cortante em vigas Gerber
O cortante funciona da mesma maneira, desenhamos ignorando o trecho Gerber e retirando o apoio extremo e a rótula da esquerda, tendo o seguinte gráfico

Já sabemos que separar o trecho Gerber nos mostra que podemos ignorar tudo a partir da segunda rótula, então teremos que

Método Gráfico de Reação de apoio em vigas Gerber
Para reação de apoio seguimos a mesma sequencia
Para reação de apoio em A
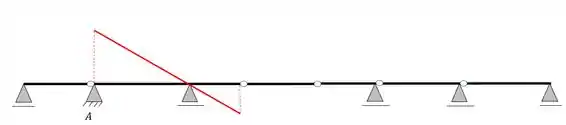
Agora basta fechar, lembrando, que nesse caso, do lado esquerdo teremos que fechar no apoio extremo, pois toda carga unitária colocada nesse trecho, produz reação de apoio em A

E se pedirmos em B? mesma coisa, fazemos ignorando os trechos com rótula
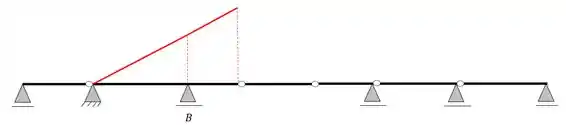
Nesse caso vemos que o apoio da esquerda já é zero, precisando fechar apenas na rótula da direita
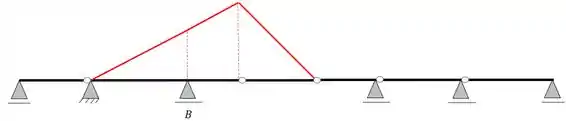
E essas serão as suas linhas de influência.
Método Gráfico de Momento e cortante na seção Gerber da viga
Esse é bem simples, porque imagine que tiremos o trecho Gerber da nossa seção, com ele separado teremos que
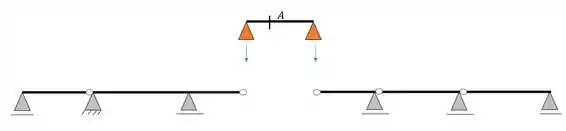
Veja que a única forma de termos momento fletor em A, ou cortante, é se aplicarmos um carga unitária na própria seção Gerber, se aplicarmos em qualquer outro ponto da viga o momento fletor em A, será zero, logo a nossa linha de influência será feita apenas para o nosso trecho Gerber, que é uma viga biapoiada. Assim teremos
Para o momento
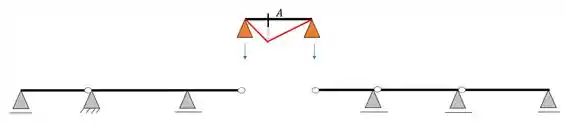
Para o cortante
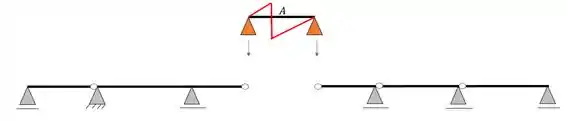
Método Gráfico de Momento e cortante no Balanço antes da seção Gerber
Por fim, imagine que coloquemos a nossa seção no balanço que tem o trecho Gerber, como mostra a figura

se é balanço, sabemos que o carregamento só afetará o balanço, não se propagando pro resto da viga a esquerda da seção, então basta fazermos o desenho ignorando a existência do trecho Gerber, e com isso teríamos
Para o momento

Para o cortante

Agora é só fazer a mesma coisa que antes, se separássemos a viga Gerber vamos ver que ela afeta o lado esquerdo, mas não afeta o lado direito, sendo afetada apenas até a segunda rótula do trecho Gerber, com isso teremos apenas que ligar o final da linha de influência na nossa rótula
Para o momento

Para o cortante

E aqui finalizamos todos os possíveis tipos de linha de influência, assim como os diferentes tipos de vigas, que o professor pode pedir na prova.
É muito importante entendermos todos os conceitos, macetes, vigas e valores que podemos determinar com as nossas vigas com Rótula interna e viga Gerber, assim como as diferenças entre as linhas de influência de cortante, momento fletor, reação de apoio e balanço.
Mas só tem uma maneira de aprendermos todos os macetes e esquemas dessa matéria, FAZENDO EXERCÍCIO. Vamos lá então???? Pra tirar o 10 redondo, precisamos exercitar bastante, bora fazer exercício!!!!!

Método Gráfico de Cortante em vigas com rótula interna
Método Gráfico de Reação de apoio em vigas com rótula interna
Método Gráfico de Momento e cortante no Balanço antes da Rótula em vigas com rótula interna
Método Gráfico de Momento e cortante no Balanço Depois da Rótula em vigas com rótula interna
Método Gráfico de momento fletor em vigas Gerber
Método Gráfico de Cortante em vigas Gerber
Método Gráfico de Reação de apoio em vigas Gerber
Método Gráfico de Momento e cortante na seção Gerber da viga
Método Gráfico de Momento e cortante no Balanço antes da seção Gerber
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine a linha de influência de momentos da viga abaixo na seção A determinada. Use o método gráfico.

Passo 1
Já sabemos que o passo a passo que iremos seguir é o seguinte:
- Primeiro marcamos a nossa seção na viga
- Depois pegamos as distâncias de cada apoio próximo a seção até a seção e rebatemos elas como raios pra baixo dos apoios
- Em seguida ligamos as pontas dessas barras em baixo dos apoios no apoio contrário
- Se houver um balanço nós prolongamos essas barras até o balanço
- Se nos balanços existirem rótulas teremos duas opções: se a rótula estiver ligada ao apoio, naquele ponto o momento será zero e não teremos prosseguimento da linha de influência. Agora, se for uma rótula de uma estrutura Gerber, iremos prolongar a linha de influência até a segunda rótula de forma a zerar quando chegar na segunda rótula.
- Feito tudo isso teremos a nossa linha de influência, e a única coisa que irá ficar faltando será calcular os valores principais dessas linhas, que iremos usar regra de 3 para calcularmos.
- Por fim, apagar as linhas de construção.
Entendido tudo isso, vamos ao cálculo da nossa linha de influência.
Passo 2
Já sabemos que o primeiro passo foi feito no próprio enunciado que marcou a seção no ponto que deveríamos calcular.
Vamos então já ir para o segundo passo onde iremos rebater as distâncias até os apoios mais próximos como vemos na figura abaixo.
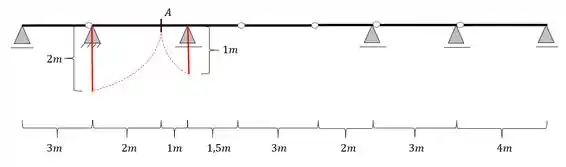
Passo 3
Como sabemos no passo a passo devemos agora ligar as extremidades de cada barra rebatida no apoio contrário, e dessa forma teremos que as linhas ficarão
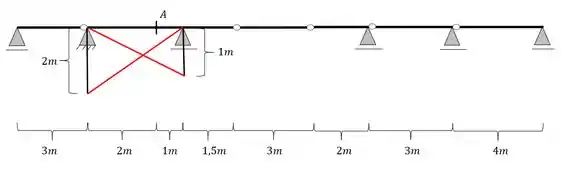
Passo 4
Para o próximo passo podemos ver que a nossa barra possui um balanço no seu lado direito, que vai até uma estrutura Gerber, ou seja, no caso do balanço da direita iremos prolongar até a primeira rótula e depois, da primeira rótula iremos descer até zero na segunda rótula. Já do lado esquerdo o balanço tem uma rotula que termina em um apoio, ou seja, nesse ponto a nossa linha de influencie para, e não tem prosseguimento, dessa forma, nossa estrutura ficará
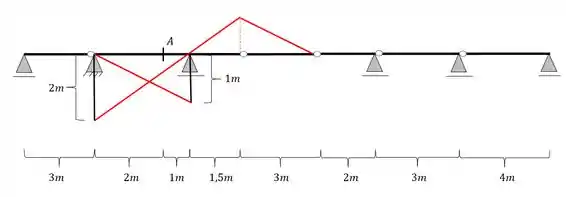
Passo 5
Agora já podemos fazer a regra de 3 levando em consideração os seguintes triangulos
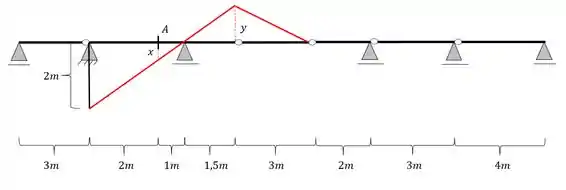
Teremos aqui a seguinte regra de 3, calculando primeiro y
Calculando agora x, teremos o seguinte
Ou seja, calculamos os valores pertinentes da nossa linha de influência
Passo 6
Agora que já fizemos tudo basta apagarmos as nossas linhas de construção, e o que irá sobrar será exatamente a nossa linha de influência da viga
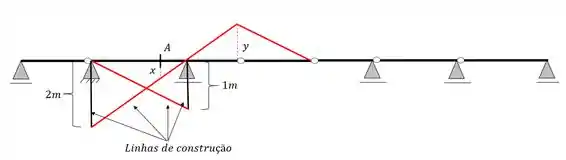
Apagando essas linhas e acrescentando os valores calculados na regra de 3 teremos a seguinte linha de influencia

Resposta
Linha de Influência de momentos fletores na seção A por métodos gráficos

Exercício Resolvido #2
Elaboração Própria
Determine a linha de influência de cortantes da viga abaixo na seção A determinada. Use o método gráfico.

Passo 1
Já sabemos que o passo a passo que iremos seguir é o seguinte:
- Primeiro marcamos a nossa seção na viga
- Depois descemos uma reta de valor unitário no apoio mais próximo a esquerda da nossa seção e subimos uma reta de valor unitário no apoio mais próximo à direita.
- Em seguida ligamos as pontas dessas retas nos apoios contrários mais próximos
- Se houver um balanço nós prolongamos essas retas até o balanço.
- Se nos balanços existirem rótulas teremos duas opções: se a rótula estiver ligada ao apoio, naquele ponto o cortante será zero e não teremos prosseguimento da linha de influência. Agora, se for uma rótula de uma estrutura Gerber, iremos prolongar a linha de influência até a segunda rótula de forma a zerar quando chegar na segunda rótula.
- Por fim, sabemos que devemos ligar as duas retas paralelas que chegam nos apoios por uma transversal que passa pela seção calculada.
- Feito tudo isso teremos a nossa linha de influência, e a única coisa que irá ficar faltando será calcular os valores principais dessas linhas, que iremos usar regra de 3 para calcularmos.
- Por fim, apagar as linhas de construção.
Entendido tudo isso, vamos ao cálculo da nossa linha de influência.
Passo 2
Já sabemos que o primeiro passo foi feito no próprio enunciado que marcou a seção no ponto que deveríamos calcular.
Vamos então já ir para o segundo passo onde iremos descer e subir uma reta de valor unitário em cada uns dos apoios mais próximos da nossa seção, seguindo o sentido do passo a passo, ou seja, pra baixo na esquerda e pra cima na direita.
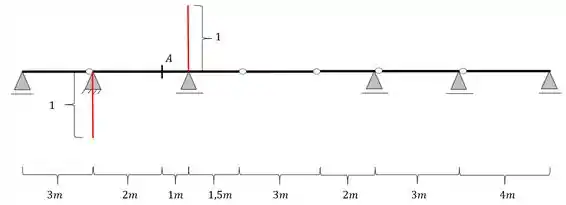
Passo 3
Como sabemos no passo a passo devemos agora ligar as extremidades de cada reta no apoio contrário, e dessa forma teremos que as linhas ficarão
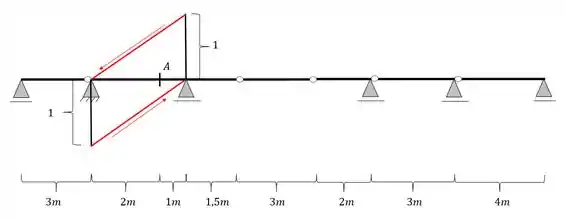
Passo 4
Para o próximo passo podemos ver que a nossa barra possui um balanço no seu lado direito, que vai até uma estrutura Gerber, ou seja, no caso do balanço da direita iremos prolongar até a primeira rótula e depois, da primeira rótula iremos descer até zero na segunda rótula. Já do lado esquerdo o balanço tem uma rotula que termina em um apoio, ou seja, nesse ponto a nossa linha de influencie para, e não tem prosseguimento, dessa forma, nossa estrutura ficará
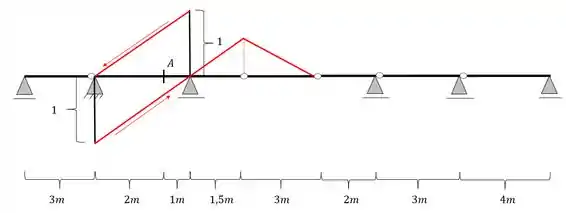
Passo 5
Agora iremos passar a nossa reta transversal, ligando as retas paralelas que passam nos apoios, passando pela nossa seção A que está sendo calculada, dessa forma teremos a seguinte estrutura
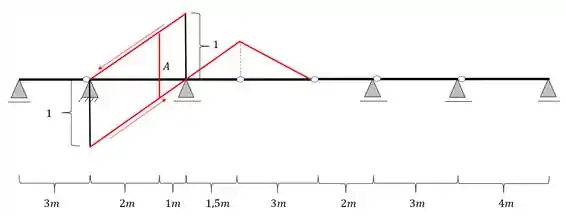
Passo 6
Agora já podemos fazer as 2 regras de 3 levando em consideração os seguintes triângulos
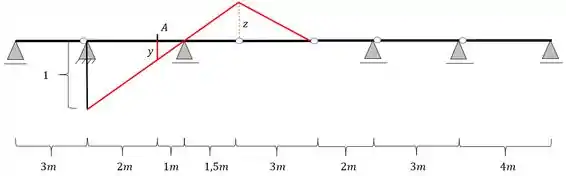
Teremos aqui a seguinte regra de 3, calculando primeiro x
Calculando agora Y, teremos o seguinte
Calculando agora Z, teremos o seguinte
E somando Y+x teremos exatamente o valor central que tem que dar 1 já que as nossas retas são paralelas
O que comprova que de fato fizemos tudo certo já que o valor central está mantido em 1.
Passo 7
Agora que já fizemos tudo basta apagarmos as nossas linhas de construção, e o que irá sobrar será exatamente a nossa linha de influência da viga
Apagando essas linhas e acrescentando os valores calculados na regra de 3 teremos a seguinte linha de influencia

Resposta
Linha de Influência de cortantes na seção A por métodos gráficos.

Exercício Resolvido #3
Elaboração Própria
Determine a linha de influência de reação de apoio da viga abaixo no apoio A determinada. Use o método gráfico.

Passo 1
Já sabemos que o passo a passo que iremos seguir é o seguinte:
- Primeiro iremos levantar uma reta de tamanho unitário em cima do apoio em que foi pedido a linha de influência.
- Depois iremos ligar o topo da reta ao apoio contrário
- Feito isso, iremos prolongar a reta para cada um dos balanços que houver
- Se nos balanços existirem rótulas teremos duas opções: se a rótula estiver ligada ao apoio, naquele ponto o cortante será zero e não teremos prosseguimento da linha de influência. Agora, se for uma rótula de uma estrutura Gerber, iremos prolongar a linha de influência até a segunda rótula de forma a zerar quando chegar na segunda rótula.
- Depois basta fazer a regra de 3 e apagar as linhas de construção.
Entendido tudo isso, vamos ao cálculo da nossa linha de influência.
Passo 2
Vamos ao primeiro passo que consiste em subir uma reta de valor unitário bem em cima do nosso apoio
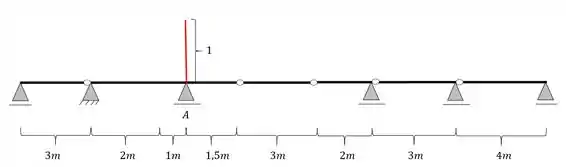
Passo 3
Em seguida devemos ligar o topo da nossa reta unitária no apoio contrário, como mostra a figura
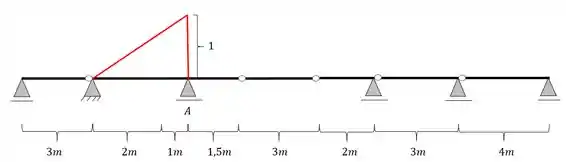
Passo 4
Por fim fazemos os devidos prolongamentos da nossa reta, para cada lado dos balanços que temos. Podemos ver que a nossa barra possui um balanço no seu lado direito, que vai até uma estrutura Gerber, ou seja, no caso do balanço da direita iremos prolongar até a primeira rótula e depois, da primeira rótula iremos descer até zero na segunda rótula. Já do lado esquerdo o balanço tem uma rotula que termina em um apoio, ou seja, nesse ponto a nossa linha de influencie para, e não tem prosseguimento, dessa forma, nossa estrutura ficará
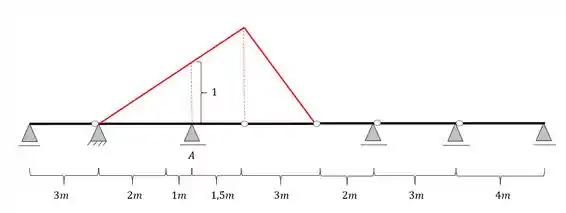
Agora só falta a regra de 3.
Passo 5
Usaremos para a nossa regra de 3 os seguintes triângulos
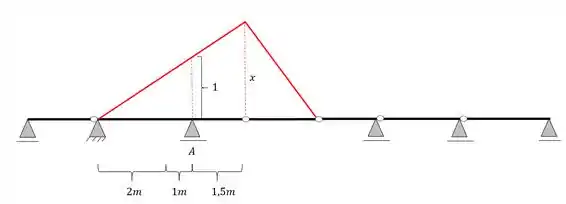
Teremos aqui a seguinte regra de 3, calculando x
Passo 6
Agora que já fizemos tudo basta apagarmos as nossas linhas de construção, e o que irá sobrar será exatamente a nossa linha de influência da viga
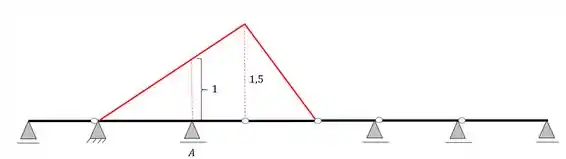
Apagando essas linhas e acrescentando os valores calculados na regra de 3 teremos a seguinte linha de influencia
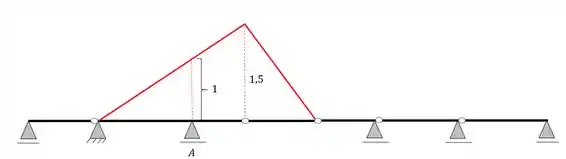
Resposta
Linha de Influência de reação do apoio A.
Exercício Resolvido #4
Elaboração Própria
Determine a linha de influência de momento fletor da viga abaixo na seção A determinada. Use o método gráfico.
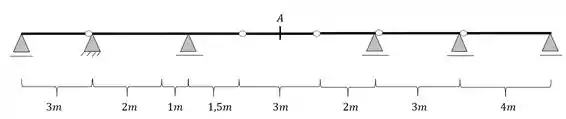
Passo 1
Já sabemos que o passo a passo que iremos seguir é o seguinte:
- Primeiro marcamos a nossa seção na viga
- Depois pegamos as distâncias de cada apoio próximo a seção até a seção e rebatemos elas como raios pra baixo dos apoios
- Em seguida ligamos as pontas dessas barras em baixo dos apoios no apoio contrário
- Se houver um balanço nós prolongamos essas barras até o balanço
- Se nos balanços existirem rótulas teremos duas opções: se a rótula estiver ligada ao apoio, naquele ponto o momento será zero e não teremos prosseguimento da linha de influência. Agora, se for uma rótula de uma estrutura Gerber, iremos prolongar a linha de influência até a segunda rótula de forma a zerar quando chegar na segunda rótula.
- Feito tudo isso teremos a nossa linha de influência, e a única coisa que irá ficar faltando será calcular os valores principais dessas linhas, que iremos usar regra de 3 para calcularmos.
- Por fim, apagar as linhas de construção.
Entendido tudo isso, vamos ao cálculo da nossa linha de influência.
Passo 2
Já sabemos que o primeiro passo foi feito no próprio enunciado que marcou a seção no ponto que deveríamos calcular.
Vamos então já ir para o segundo passo onde iremos rebater as distâncias até as rótulas mais próximas, que serviram como apoios fictícios caso tivéssemos analisando a seção de forma separada, como vemos na figura abaixo.
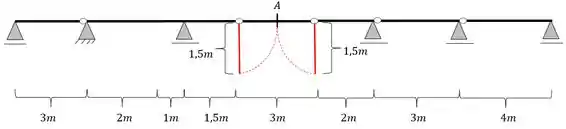
Passo 3
Como sabemos no passo a passo devemos agora ligar as extremidades de cada barra rebatida no apoio contrário, e nesse caso, na rotula contraria, e dessa forma teremos que as linhas ficarão
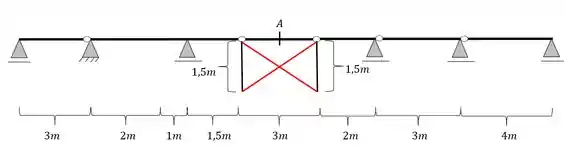
Passo 4
Para o próximo passo podemos ver que a nossa barra possui um balanço no seu lado direito e esquerdo, porém a nossa seção se encontra em um estrutura gerber, ou seja, uma estrutura que pode ser destacada de todo o resto, isso significa que se colocarmos a nossa carga unitária em qualquer outro ponto da viga, que não seja o seu vão central, ela não produzirá momentos fletores, ou seja, a nossa linha de influência zera nas rótulas.
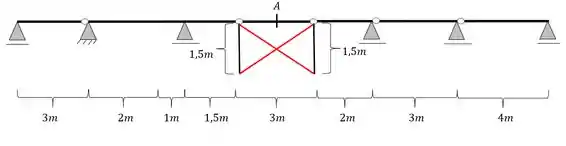
Passo 5
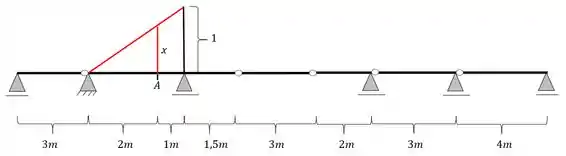
Agora já podemos fazer a regra de 3 levando em consideração os seguintes triângulos
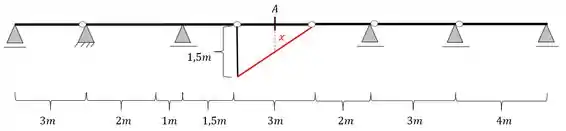
Teremos aqui a seguinte regra de 3, calculando x
Ou seja, calculamos os valores pertinentes da nossa linha de influência
Passo 6
Agora que já fizemos tudo basta apagarmos as nossas linhas de construção, e o que irá sobrar será exatamente a nossa linha de influência da viga
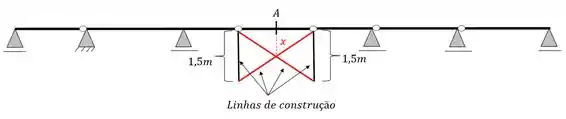
Apagando essas linhas e acrescentando os valores calculados na regra de 3 teremos a seguinte linha de influencia

Resposta
Linha de Influência de momentos fletores na seção A por métodos gráficos
