Solução de Pórticos Simples- até 3 barras por nó
Teoria
Introdução
Na parte 1 dessa aula verificamos como calcular os esforços para alguns nós desse pórtico. Agora, vamos ver como poderemos calcular o resto dos esforços desse pórtico, partindo agora para uma análise mais minuciosa dos nós dele que possuem 3 barras, assim finalizamos a parte 2 da nossa aula de pórticos simples.
Vamos nessa então!!!
Quarto passo: Valores em nós com mais de 3 barras
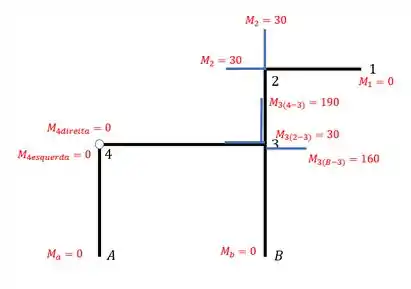
Agora temos que ir pro nosso nó de 3 barras, em que esse processo sempre será o mesmo para nós que tenham 3 ou mais barras. Nesse caso a solução consiste em analisar cada lado da barra, e depois verificar se está em equilíbrio, como assim? Vamos por partes
Primeiro, quais momentos aparecem no nó 3 vindo pela barra 2-3?
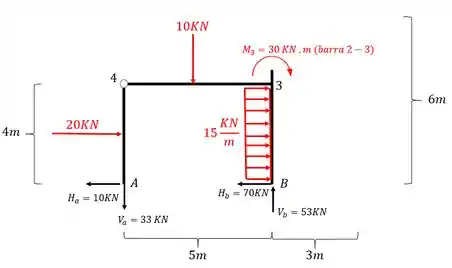
Lembrando que se quiséssemos também o normal e cisalhante deveríamos levar a carga de 10KN.
Segundo, nós precisamos também saber quais momentos aparecem no nó 3 pela barra B-3
Como está apontando pro nó, seu braço de alavanca é zero, logo, só precisamos nos preocupar com as cargas de e . Com isso teremos
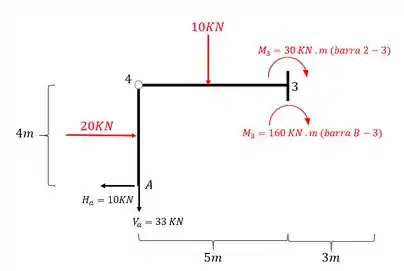
Você pode estar se perguntando qual sinal usar para os momentos. Para facilitar eu nuca coloca sinal, o que eu faço é olhar os sentidos, se estiverem no mesmo sentido eu somo, se tiverem em sentidos opostos eu subtraio, e no caso ganha o sentido que der o sinal maior, por exemplo, se eu arbitrar positivo o sentido horário, então o anti-horário seria negativo. Se eu fizer a conta e der positivo, eu seu que é horário, se der negativo, é anti-horário. Mas como saber onde desenhar no gráfico? Ai é simples, só olhar em qual lado as fibras são tracionadas. Se traciona na esquerda, eu desenho pra esquerda, se traciona na direita, eu desenho pra direita, assim ei não fico perdido nem com os sinais e nem com o diagrama.
E terceiro, quais os momentos que aparecem no nó 3 pela barra 4-3?
Fazemos o mesmo processo, e nesse caso todas as cargas e reações do apoio irão contribuir. Apenas fazendo a continha dos momentos pra vocês entenderem o que eu faço.
Como queremos os momentos teremos
Como deu negativo, sentido, anti-horário.
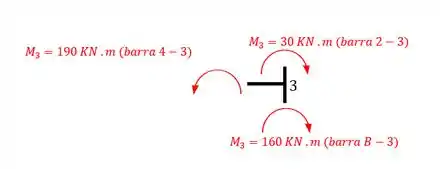
OBS: pra você nunca errar isso na prova, perceba que se somarmos tudo que estão no sentido horário com tudo eu esta no sentido anti-horário, a resposta da zero, sempre tem que dar zero, ou se tivesse algum momento concentrado no nó, teria que dar o valor desse memento. Se você fizer as contas nesse nó e a soma não zerar ou se igualar com o concentrado, está ERRADO, e você tem que refazer as contas.
Verificando as rótulas
A verificação da rótula é apenas para ver se tudo que você calculou está certo. Como você faz isso? Basta fazer o somatório de momentos pela esquerda da rótula. Se der zero ou o valor da carga concentrada na rótula, quando tiver, tudo que você fez do lado esquerdo está correto. Depois fazer a mesma coisa para o lado direito. Fazer o somatório de momentos na rótula pelo lado direito e ver se zera ou se da o valor da carga concentrada, se isso ocorrer, tudo que foi feito do lado direito, também está correto.
Somatório pela esquerda
Somatório pela direita
Quinto passo: Diagramas de momento fletor
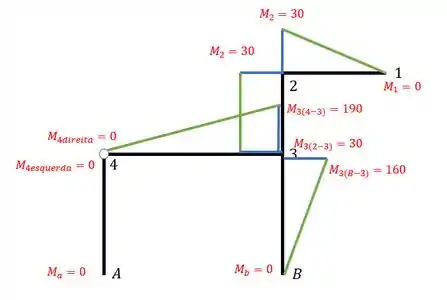
Para desenhar o diagrama é fácil. Primeiro marcamos todos os momentos que calculamos na nossa estrutura
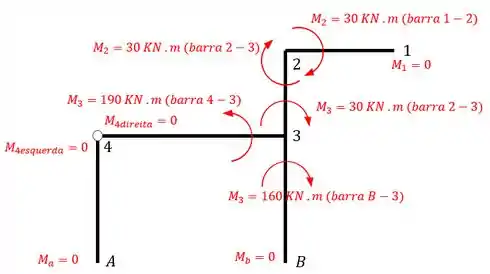
Depois que marcamos tudo fazemos uma linha perpendicular a barra na direção em que as fibras são tracionadas
Agora para saber o diagrama, basta ir na aula sobre esforços internos em vigas, que está no assunto flexão, lá ele explica como fazer momento fletor, cortante e normal para uma viga. No caos do nosso pórtico, cada barra será uma viga.
Mas também vou ensinar um macete, que é o seguinte:
Já marcamos todos os inícios e finais de momentos, só precisamos saber o que acontece no meio, pra isso olhamos cada a barra e prestamos a atenção ao seguinte:
- Se a barra só tiver a ação de carga concentrada, teremos que ela será composta apenas por retas, e o maior momento ocorrerá no ponto que tiver a carga, sendo o valor dele
- Se tiver a ação de carga distribuída, teremos que será composta por parábolas, e o maior valor ocorrerá no centro segundo a fórmula
- Agora, se tiver carga distribuída e concentrada o máximo ocorrerá entre o meio da carga distribuída e a posição da concentrada, se essa posição for em comum para os dois o máximo será dado por
- Barra 1-2 (diagrama azul claro)
- Barra 2-3 (diagrama verde)
- Barra B-3 (diagrama vermelho)
- Barra 4-3 (diagrama laranja)
- Barra A-4 (diagrama azul escuro)
- Barra B-3
- Barra 4-3
- barra 4-A
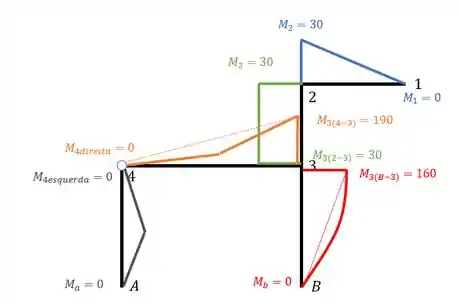
E de onde irei medir esses máximos?
Lembra que já marcamos os momentos? Vamos medir eles a partir da reta que liga esses momentos.
Todas as retas verdes serão as nossas referencias para medirmos os máximos, com isso teremos.
Vamos analisar por diagrama agora
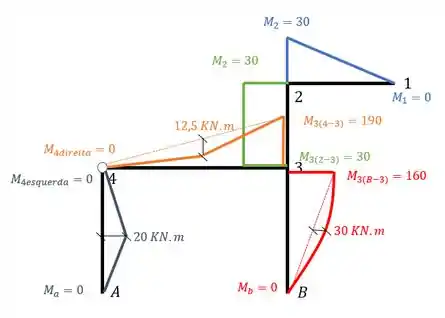
Não tem carga concentrada no meio da barra, então não muda.
não tem carga concentrada no meio da barra, então não muda.
Tem carga distribuída, então muda e teremos um máximo de
Tem carga concentrada, então muda e teremos um máximo de
Tem carga concentrada, então muda e teremos um máximo de
Marcado tudo isso no nosso diagrama, teremos
Alguns professores pedem a distancia até o eixo do pórtico, se o seu professor pedir isso, lembre-se que antes de medirmos os máximos tínhamos apenas triângulos
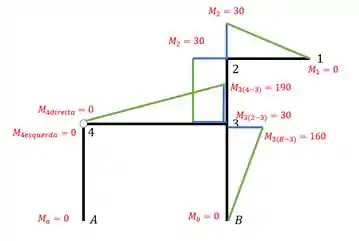
Bastaria apenas achar a distância da reta até o pórtico no ponto em que a carga está aplicada, o que conseguimos facilmente por uma regra de 3. Tendo esse valor basta somar ou subtrair o máximo que calculamos desse valor que tivermos achado na regra de 3, por exemplo, como todas as cargas estão no meio das barras, o valor de altura do triangula nessa posição é metade do que achamos para as suas extremidades, logo
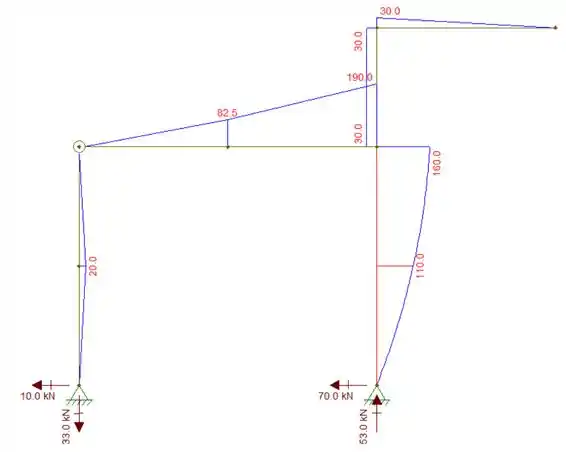
Pegando o gráfico produzido pelo programa ftool, teremos que
Ufa, agora vamos treinar isso para podermos fazer a prova bem tranquilo, vamos aos exercícios?
Verificando as rótulas
Quinto passo: Diagramas de momento fletor
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Calcule o equilíbrio no nó D do pórtico abaixo.
Passo 1
Para resolvermos qualquer exercício de pórticos simples, precisamos seguir uma sequência de passos que irá nos ajudar na solução desse tipo de problema, e a sequência é a seguinte.
- A primeira coisa que devemos fazer é o cálculo das reações de apoio, pois assim conseguiremos calcular qualquer nó sem que haja nenhum problema.
- a segunda coisa é seguir a seguinte sequência de nós a serem resolvidos:
Nós com 2 barras
Nós com 3 barras
Nós com 4 barras
...
- A terceira coisa que devemos fazer é calcular o valor dos momentos fletores, cortantes e normais em todos as barras que chegarem ou saírem de algum nó
- O quarto e último passo consiste em desenhar os diagramas do pórtico quando esse for pedido.
Agora que já sabemos qual sequência de passos devemos seguir, vamos aplicar esse conhecimento ao nosso problema.
Passo 2
Como vimos, a primeira coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em E vindo pela esquerda, teremos que
Logo
Relacionando os sistemas teremos que
logo
Conhecendo conhecemos também , substituindo, teremos
Sabemos que quando encontramos negativo significa que basta invertemos o vetor para calcularmos o valor positivo.
Por fim, podemos determinar o valor de , substituindo teremos
E dessa forma terminamos o primeiro passo que consiste em determinar o valor das reações de apoio. Vamos então ao próximo passo.
Passo 2
Como vimos, o segundo passo diz para resolvermos os nós com duas barras e se você notar, já resolvemos esses nós no exercício correspondente a esse, mas na parte 1 dessa aula, vamos agora resolver o nó que possui 3 barras, e que de fato corresponde a parte 2 dessa aula.
Sabemos que a primeira coisa que devemos fazer é cortar o pórtico no nó que iremos calcular e levarmos até esse nó todos os esforços que foram descartados com o corte do pórtico, vamos lá então.
Perceba que o corte que faremos irá dispensar todos os carregamentos e reações de apoio do nosso pórtico, logo, devemos levar para o nó tudo aquilo que seria perdido com a retirada dessas cargas, com isso vamos fazer cada braço do nó D de cada vez.
Passo 3
Primeiro o braço a direita do nó D, retirando todo aquele lado e levando suas cargas e respectivos momentos, teremos que
Juntando todos os carregamentos na mesma direção, teremos que
Vemos que ao olharmos o nó D pelo lado direito, teremos, na barra CD um cortante de 400 KN, um normal de tração de 150KN e um momento fletor de 2100 KN.m. Conhecido isso, vamos analisar o nó D, mas agora vindo da parte de cima da barra.
Passo 4
Vindo pela parte de cima do nó D, retirando toda aquela parte e levando suas cargas e respectivos momentos, teremos que
Vemos que ao olharmos o nó D vindo por cima, teremos, na barra ED um cortante de 463,64 KN e um momento fletor de 1159,1 KN.m. Conhecido isso, vamos analisar o nó D, mas agora vindo da parte de baixo da barra.
Passo 5
Vindo pela parte de baixo do nó D, retirando toda aquela parte e levando suas cargas e respectivos momentos, teremos que
Vemos que ao olharmos o nó D vindo por baixo, teremos, na barra GD um cortante de 313,64 KN e um momento fletor de 940,9 KN.m, e além disso temos um normal de 400KN. Vamos então fazer o equilíbrio do nó D.
Passo 6
Fazendo o equilíbrio teremos que
Podemos ver então que o nó D está equilibrado, basta olharmos o equilíbrio do nó
Logo, o nó D está equilibrado.
Resposta
Equilíbrio do nó D
Exercício Resolvido #2
Elaboração Própria
Calcule o valor do momento fletor no nó C do pórtico abaixo.
Passo 1
Para resolvermos qualquer exercício de pórticos simples, precisamos seguir uma sequência de passos que irá nos ajudar na solução desse tipo de problema, e a sequência é a seguinte.
- A primeira coisa que devemos fazer é o cálculo das reações de apoio, pois assim conseguiremos calcular qualquer nó sem que haja nenhum problema.
- a segunda coisa é seguir a seguinte sequência de nós a serem resolvidos:
Nós com 2 barras
Nós com 3 barras
Nós com 4 barras
...
- A terceira coisa que devemos fazer é calcular o valor dos momentos fletores, cortantes e normais em todos as barras que chegarem ou saírem de algum nó
- O quarto e último passo consiste em desenhar os diagramas do pórtico quando esse for pedido.
Agora que já sabemos qual sequência de passos devemos seguir, vamos aplicar esse conhecimento ao nosso problema.
Passo 2
Como vimos, a primeira coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em D vindo pela direita, teremos que
Logo
Relacionando os sistemas teremos que
logo
Isolando teremos
Isolando do outro sistema teremos que
Tendo os valores de e basta substituirmos no terceiro sistema, que é dado por
Substituindo as próximas reações de apoios teremos que
Agora que já temos as reações de apoio, vamos ao equilíbrio do nó C.
Passo 2
Como vimos, o segundo passo diz para resolvermos os nós com duas barras e se você notar, já resolvemos esses nós no exercício correspondente a esse, mas na parte 1 dessa aula, vamos agora resolver o nó que possui 3 barras, e que de fato corresponde a parte 2 dessa aula.
Sabemos que a primeira coisa que devemos fazer é cortar o pórtico no nó que iremos calcular e levarmos até esse nó todos os esforços que foram descartados com o corte do pórtico, vamos lá então.
Perceba que o corte que faremos irá dispensar todos os carregamentos e reações de apoio do nosso pórtico, logo, devemos levar para o nó tudo aquilo que seria perdido com a retirada dessas cargas, com isso vamos fazer cada braço do nó C de cada vez.
Passo 3
Primeiro o braço de cima do nó C, retirando toda a parte de cima e levando suas cargas e respectivos momentos, teremos que
Juntando todos os carregamentos na mesma direção, teremos que
Vemos que ao olharmos o nó C por cima, teremos, na barra CD um cortante de 127,41 KN, um normal de compressão de 73,83 KN e um momento fletor de 700,74 KN.m. Conhecido isso, vamos analisar o nó C, mas agora vindo da parte de baixo da barra.
Passo 4
Vindo pela parte de baixo do nó C, retirando toda aquela parte e levando suas cargas e respectivos momentos, teremos que
Vemos que ao olharmos o nó C vindo por baixo, teremos, na barra temos um cortante de 240 KN e um momento fletor de 720 KN.m. Conhecido isso, vamos analisar o nó C, mas agora vindo da parte esquerda da barra.
Passo 5
Vindo pela esquerda do nó C, retirando toda aquela parte e levando suas cargas e respectivos momentos, teremos que
Juntando os carregamentos com mesmo direcionamento, teremos que
Vemos que ao olharmos o nó C vindo pela esquerda, teremos, na barra BC um cortante de 73,83 KN e um momento fletor de 1420,74 KN.m, e além disso temos um normal de 112,59 KN. Vamos então fazer o equilíbrio do nó C.
Passo 6
Fazendo o equilíbrio teremos que
Podemos ver então que o nó C está equilibrado, basta olharmos o equilíbrio do nó
Logo, o nó C está equilibrado.
Resposta
Equilíbrio do nó C
