Pórticos com tirantes e cabos
Teoria
Introdução
Já vimos até aqui como resolver pórticos simples e pórticos compostos. Porém, ainda a um terceiro conceito que é muito importante entendermos, que é o conceito de pórticos com tirantes ou cabos. Vamos então entender como funciona esse conceito
- Tirantes
- Cabos
- Número de equações
- Número de incógnitas
- O primeiro é que sabemos que cortar a rótula nos permite ter um apoio do segundo gênero
- O segundo é que como sabemos que o tirante só possui esforço normal, então basta substituir a barra cortada por uma força normal, como fazíamos na treliça quando usávamos o método da seção de Richter. Logo, quando cortarmos o nosso pórtico nós teremos.
Tirantes são barras que funcionam apenas tracionadas ou comprimidas, como as treliças, com a diferença que o tirante é uma parra no pórtico que só tem atuação de esforços normais, e, nesse caso, não possui ação de esforços fletores e cisalhantes. algo que é um macete é procurar as barrar que possuam rotulas de ambos os lados, pois assim a barra seria como uma barra de treliça que só tem normal, poréeeeemmm, deve-se tomar muito cuidado, pois se tiver algum momento concentrado nessa barra, ou ainda, um carregamento, essa barra terá um cisalhante e um fletor, e não será um tirante, por mais que tenha rótulas de ambos os lados.
Cabos, assim como tirantes, estão sujeitos apenas a ação do esforço normal, porém, cabos tem baixíssima resistência a ação da compressão, enquanto alta resistência a tração. Ou seja, diferente dos tirantes que atuam tanto na compressão quanto na tração, os cabos só aturam na tração.
Agora que entendemos como funciona o conceito, é necessário entender como funciona a solução, pois a pergunta principal é: o que o meu professor pode cobrar na prova?
Situação
Vamos pensar que chegamos na prova, e seu professor colocou o seguinte pórtico.
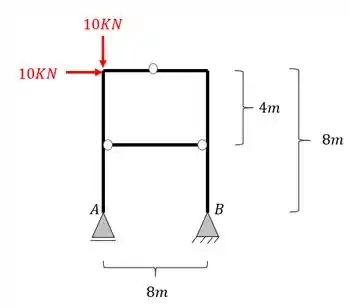
Como já sabemos desenhar o diagrama de pórticos simples, vamos entender como calcular o valor apenas do tirante, ou seja, a pergunta na prova seria: qual a tensão normal nesse tirante? E explique se esse tirante poderia ser substituído por um cabo.
Não da pra saber se dá felicidade ou tristeza quando o professor pede só o tirante, mas vamos ver no passo a passo como é bem simples resolver esse tipo de questão
Passo 1: Balanceamento de incógnitas e equações
Sabemos que antes de qualquer coisa devemos balancear nosso pórtico para saber de que tipo de estrutura ele se trata, então vamos fazer isso
Para o número de equações nós temos
Para o número de incógnitas nós temos
Ou seja, como o número de incógnitas é igual ao número de equações, nosso pórtico é simples, do tipo, isostático.
Passo 2: Cálculo das reações de apoio
Como já sabemos, sempre devemos saber as reações de apoio antes de qualquer coisa, então para o nosso pórtico, substituindo os apoios teremos
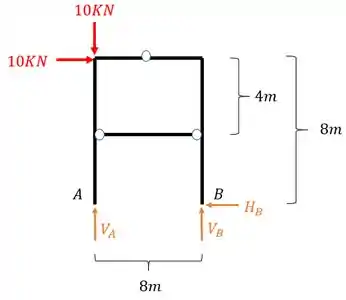
Usando as fórmulas de equilíbrio teremos
Ou seja, a nossa estrutura com as reações ficará
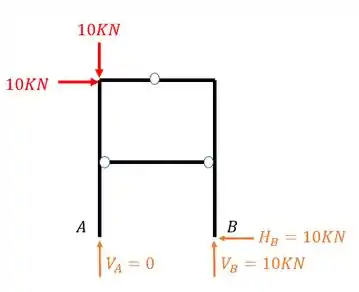
Passo 3: E o que eu faço com o tirante?
Ai que entra a nossa rótula, lembra que temos 4 equações? Nós usamos 3 de equilíbrio, faltam nesse caso apenas 1, que tem a ver com a rótula. Perceba que quando olhamos o pórtico como um todo, fica muito difícil entender o que fazer com o tirante. Por isso nesse caso é muito mais fácil cortar o pórtico ao meio, passando exatamente pela rótula, por dois motivos.
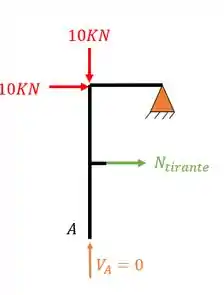
Com isso, sabemos que no apoio fictício o nosso somatório de momentos deve ser zero, escrevendo essa ultima equação teremos
- Calcular reações de apoio
- Achar o pórtico simples
- Calcular o tirante ou cabo (quando houver)
- Por fim, desenhar o diagrama.
Ou seja, podemos dizer que o nosso tirante está sofrendo uma compressão (pois lembre-se que sempre adotamos o positivo tracionando a peça, como deu negativo, sabemos que está comprimindo a peça).
Isso nos ajuda a responder a próxima pergunta: poderíamos substituir o tirante por um cabo?
De jeito nenhum, cabos não possuem nenhuma resistência a compressão, como vimos nosso tirante está comprimindo, então é inviável o uso do cabo nesse caso.
OBS:. É bem legal ver que com o pórtico dividido, é possível determinar as reações do apoio fictício. Essas reações de apoio irão nos ajudar nó cálculo do esforço normal e do cisalhante no pórtico, ou seja, a questão poderia ser um pouco mais complexa se pedisse os diagramas. Mas se você parar pra ver, o pórtico dividido ao meio, com o tirante já calculado, vira nada mais que um pórtico simples, que já estamos cansados de saber calcular. Pra resumir, sempre que for pedido para calcular os diagramas, tem que seguir os seguintes passos
- Passo 4: E o que eu faço quando tem um tirante em um pórtico composto?
Vamos analisar o que fazer no caso abaixo, e a partir dele ficará mais fácil saber o que fazer em um pórtico composto com tirante.
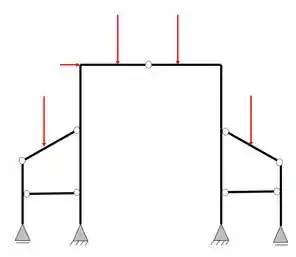
Sabemos que os pórticos compostos são uma composição de pórticos simples, e nesse caso, vemos que os pórticos simples laterais além de estarem ligados por rótulas, estão ligados por tirantes, como resolver nesse caso? O passo a passo é o mesmo que vimos no primeiro exemplo
- Reações de apoio
- Nesse caso para separarmos os pórticos simples precisaremos cortar a rótula e o tirante
- Substituir a rótula cortada por um apoio do segundo gênero e o tirante por um esforço normal.
fazendo o passo a passo acima temos o seguinte pórtico dividido
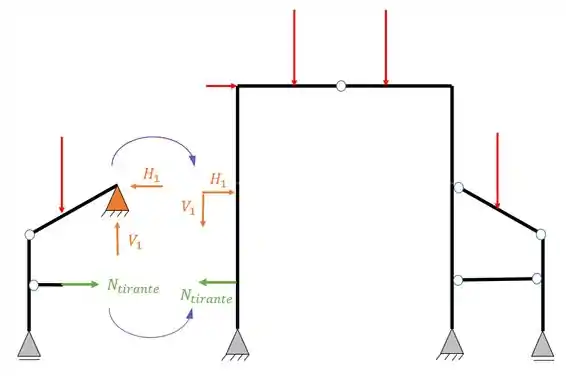
Olha que legal quando olhamos somente o nosso pórtico simples lateral que foi separado
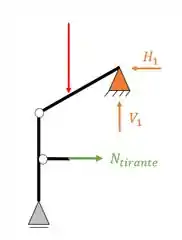
Se fizermos um balanceamento de equações e incógnitas teremos
Lembrando que o número de equações por rótula é igual ao número de barras naquela rótula menos um. Como na rótula do tirante só sai uma barra, dessa rótula não teremos nenhuma equação.
Incógnitas = (2 reações do segundo gênero) + (1 reação do primeiro gênero) + (1 tirante) = 4
Ou seja, se temos 4 incógnitas e 4 equações, e além disso temos 1 vetor em cada direção, nosso pórtico simples é isostático e sabemos resolver facilmente.
Então basicamente temos que ver o seguinte.
- Tirantes e cabos funcionam somente a tração e compressão, sendo os cabos estritamente restritos a tração.
- Quando cortamos uma rótula ganhamos um apoio do segundo gênero
- Quando cortamos um tirante ou cabo ganhamos um esforço normal
- Em pórticos compostos precisamos dividir em pórticos simples, respeitando tudo que foi falado acima.
- Precisamos sempre fazer o balanceamento do número de incógnitas e equações dos pórticos simples
- Precisamos calcular primeiro sempre as reações de apoio
Então isso tudo resume os cuidados que temos que ter com tirantes e cabos, vamos agora fazer bastante exercício pra não errarmos bobeira na prova, e sabermos resolver qualquer coisa que os professores possam pedir, bora lá?
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine o valor do Normal no Tirante do pórtico dado abaixo
Passo 1
Como já sabemos, precisamos fazer um passo a passo para sabermos como resolveremos o nosso problema, e o passo a passo é
- A primeira coisa que faremos é um balanceamento de incógnitas e equações e iremos confirmar se a nossa estrutura é isostática, sendo isostática iremos ao próximo passo do nosso problema.
- A segunda coisa que iremos fazer é o cálculo das reações de apoio do nosso problema
- Como o objetivo é determinar o normal no tirante, basta escolhermos com sabedoria um ponto para fazermos o somatório de momentos de forma que a força exercida na estrutura pelo tirante seja uma incógnita, e como já iremos ter determinado as reações de apoios no passo anterior, a força no tirante será a única incógnita, e dessa forma iremos determinar as forças no tirante.
Vamos aplicar o nosso passo a passo no exercício? Vamos lá.
Passo 2
Como vimos, o primeiro passo consiste em fazermos um balanceamento de incógnitas e equações, sabemos que primeiro devemos fazer um balanceamento de incógnitas, e para isso contabilizamos reações de apoios e o nosso tirante, dessa forma teremos que
Fazendo a contabilidade teremos
Ou seja, temos 4 incógnitas no nosso problema.
Passo 3
Vamos agora a contabilização do número de equações.
Sabemos que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Ou seja, podemos dizer que o número de equações do nosso problema é igual ao número de incógnitas, ou seja, temos um problema isostático, sendo assim, podemos ir para o próximo passo do nosso passo a passo, que é resolver as reações de apoio do nosso pórtico.
Passo 4
Como vimos, a segunda coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E assim terminamos as reações de apoio, vamos a determinação da força no tirante que é o nosso último passo.
Passo 5
Vamos ao último passo que consiste em definir o normal no nosso tirante, e pra isso iremos usar como auxilio a nossa rótula.
Agora é importante que você lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, por cima ou por baixo tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em C vindo por cima, teremos que
Precisamos trocar o nosso tirante por forças normais na estrutura
E agora precisamos levar os carregamentos de cima da rótula até a rótula
Fazendo o somatório de momentos na rótula teremos que
Logo a força no nosso tirante não necessitou, nesse caso, das reações de apoio, mas, em alguns casos as reações de apoio serão de suma importância na conta, com isso força no nosso tirante é uma força de tração de intensidade 600KN
Resposta
Exercício Resolvido #2
Elaboração Própria
Determine o valor do Normal no Tirante do pórtico dado abaixo
Passo 1
Como já sabemos, precisamos fazer um passo a passo para sabermos como resolveremos o nosso problema, e o passo a passo é
- A primeira coisa que faremos é um balanceamento de incógnitas e equações e iremos confirmar se a nossa estrutura é isostática, sendo isostática iremos ao próximo passo do nosso problema.
- A segunda coisa que iremos fazer é o cálculo das reações de apoio do nosso problema
- Como o objetivo é determinar o normal no tirante, basta escolhermos com sabedoria um ponto para fazermos o somatório de momentos de forma que a força exercida na estrutura pelo tirante seja uma incógnita, e como já iremos ter determinado as reações de apoios no passo anterior, a força no tirante será a única incógnita, e dessa forma iremos determinar as forças no tirante.
Vamos aplicar o nosso passo a passo no exercício? Vamos lá.
Passo 2
Como vimos, o primeiro passo consiste em fazermos um balanceamento de incógnitas e equações, sabemos que primeiro devemos fazer um balanceamento de incógnitas, e para isso contabilizamos reações de apoios e o nosso tirante, dessa forma teremos que
Fazendo a contabilidade teremos
Ou seja, temos 4 incógnitas no nosso problema.
Passo 3
Vamos agora a contabilização do número de equações.
Sabemos que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Ou seja, podemos dizer que o número de equações do nosso problema é igual ao número de incógnitas, ou seja, temos um problema isostático, sendo assim, podemos ir para o próximo passo do nosso passo a passo, que é resolver as reações de apoio do nosso pórtico.
Passo 4
Como vimos, a segunda coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E assim terminamos as reações de apoio, vamos a determinação da força no tirante que é o nosso último passo.
Passo 5
Vamos ao último passo que consiste em definir o normal no nosso tirante, e pra isso iremos usar como auxilio a nossa rótula.
Agora é importante que você lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, por cima ou por baixo tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em C vindo por baixo, teremos que
E o ponto C será
Precisamos trocar o nosso tirante por forças normais na estrutura
E agora precisamos levar os carregamentos de baixo da rótula até a rótula
Fazendo o somatório de momentos na rótula teremos que
Logo a força no nosso tirante necessitou, nesse caso, das reações de apoio, mas, em alguns casos as reações de apoio não serão de suma importância na conta, com isso força no nosso tirante é uma força de compressão de intensidade -1980KN
Resposta
Exercício Resolvido #3
Elaboração Própria
Determine o valor do Normal no Tirante do pórtico dado abaixo
Passo 1
Como já sabemos, precisamos fazer um passo a passo para sabermos como resolveremos o nosso problema, e o passo a passo é
- A primeira coisa que faremos é um balanceamento de incógnitas e equações e iremos confirmar se a nossa estrutura é isostática, sendo isostática iremos ao próximo passo do nosso problema.
- A segunda coisa que iremos fazer é o cálculo das reações de apoio do nosso problema
- Como o objetivo é determinar o normal no tirante, basta escolhermos com sabedoria um ponto para fazermos o somatório de momentos de forma que a força exercida na estrutura pelo tirante seja uma incógnita, e como já iremos ter determinado as reações de apoios no passo anterior, a força no tirante será a única incógnita, e dessa forma iremos determinar as forças no tirante.
Vamos aplicar o nosso passo a passo no exercício? Vamos lá.
Passo 2
Como vimos, o primeiro passo consiste em fazermos um balanceamento de incógnitas e equações, sabemos que primeiro devemos fazer um balanceamento de incógnitas, e para isso contabilizamos reações de apoios e o nosso tirante, dessa forma teremos que
Fazendo a contabilidade teremos
Ou seja, temos 4 incógnitas no nosso problema.
Passo 3
Vamos agora a contabilização do número de equações.
Sabemos que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Ou seja, podemos dizer que o número de equações do nosso problema é igual ao número de incógnitas, ou seja, temos um problema isostático, sendo assim, podemos ir para o próximo passo do nosso passo a passo, que é resolver as reações de apoio do nosso pórtico.
Passo 4
Como vimos, a segunda coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E sabemos que quando da negativo, podemos, nesse caso, inverter o nosso vetor para podermos usá-lo com sinal positivo.
E assim terminamos as reações de apoio, vamos a determinação da força no tirante que é o nosso último passo.
Passo 5
Vamos ao último passo que consiste em definir o normal no nosso tirante, e pra isso iremos usar como auxilio a nossa rótula.
Agora é importante que você lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, por cima ou por baixo tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em C vindo por baixo, teremos que
E o ponto C será
Precisamos trocar o nosso tirante por forças normais na estrutura
E agora precisamos levar os carregamentos de baixo da rótula até a rótula
Fazendo o somatório de momentos na rótula teremos que
Logo a força no nosso tirante necessitou, nesse caso, das reações de apoio, mas, em alguns casos as reações de apoio não serão de suma importância na conta, com isso força no nosso tirante é uma força de tração de intensidade 1720 KN
Resposta
Exercício Resolvido #4
Elaboração Própria
Determine o valor do Normal no Tirante do pórtico dado abaixo
Passo 1
Como já sabemos, precisamos fazer um passo a passo para sabermos como resolveremos o nosso problema, e o passo a passo é
- A primeira coisa que faremos é um balanceamento de incógnitas e equações e iremos confirmar se a nossa estrutura é isostática, sendo isostática iremos ao próximo passo do nosso problema.
- A segunda coisa que iremos fazer é o cálculo das reações de apoio do nosso problema
- Como o objetivo é determinar o normal no tirante, basta escolhermos com sabedoria um ponto para fazermos o somatório de momentos de forma que a força exercida na estrutura pelo tirante seja uma incógnita, e como já iremos ter determinado as reações de apoios no passo anterior, a força no tirante será a única incógnita, e dessa forma iremos determinar as forças no tirante.
Vamos aplicar o nosso passo a passo no exercício? Vamos lá.
Passo 2
Como vimos, o primeiro passo consiste em fazermos um balanceamento de incógnitas e equações, sabemos que primeiro devemos fazer um balanceamento de incógnitas, e para isso contabilizamos reações de apoios e o nosso tirante, dessa forma teremos que
Fazendo a contabilidade teremos
Ou seja, temos 4 incógnitas no nosso problema.
Passo 3
Vamos agora a contabilização do número de equações.
Sabemos que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Ou seja, podemos dizer que o número de equações do nosso problema é igual ao número de incógnitas, ou seja, temos um problema isostático, sendo assim, podemos ir para o próximo passo do nosso passo a passo, que é resolver as reações de apoio do nosso pórtico.
Passo 4
Como vimos, a segunda coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E assim terminamos as reações de apoio, vamos a determinação da força no tirante que é o nosso último passo.
Passo 5
Vamos ao último passo que consiste em definir o normal no nosso tirante, e pra isso iremos usar como auxilio a nossa rótula.
Agora é importante que você lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, por cima ou por baixo tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em C vindo por baixo, teremos que
E o ponto C será
Precisamos trocar o nosso tirante por forças normais na estrutura
E agora precisamos levar os carregamentos de baixo da rótula até a rótula
Fazendo o somatório de momentos na rótula teremos que
Logo a força no nosso tirante necessitou, nesse caso, das reações de apoio, mas, em alguns casos as reações de apoio não serão de suma importância na conta, com isso força no nosso tirante é uma força de tração de intensidade 114,2 KN
Resposta
Exercício Resolvido #5
Elaboração Própria
Determine o valor do Normal no Tirante do pórtico dado abaixo
Passo 1
Como já sabemos, precisamos fazer um passo a passo para sabermos como resolveremos o nosso problema, e o passo a passo é
- A primeira coisa que faremos é um balanceamento de incógnitas e equações e iremos confirmar se a nossa estrutura é isostática, sendo isostática iremos ao próximo passo do nosso problema.
- A segunda coisa que iremos fazer é o cálculo das reações de apoio do nosso problema
- Como o objetivo é determinar o normal no tirante, basta escolhermos com sabedoria um ponto para fazermos o somatório de momentos de forma que a força exercida na estrutura pelo tirante seja uma incógnita, e como já iremos ter determinado as reações de apoios no passo anterior, a força no tirante será a única incógnita, e dessa forma iremos determinar as forças no tirante.
Vamos aplicar o nosso passo a passo no exercício? Vamos lá.
Passo 2
Como vimos, o primeiro passo consiste em fazermos um balanceamento de incógnitas e equações, sabemos que primeiro devemos fazer um balanceamento de incógnitas, e para isso contabilizamos reações de apoios e o nosso tirante, dessa forma teremos que
Fazendo a contabilidade teremos
Ou seja, temos 4 incógnitas no nosso problema.
Passo 3
Vamos agora a contabilização do número de equações.
Sabemos que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Ou seja, podemos dizer que o número de equações do nosso problema é igual ao número de incógnitas, ou seja, temos um problema isostático, sendo assim, podemos ir para o próximo passo do nosso passo a passo, que é resolver as reações de apoio do nosso pórtico.
Passo 4
Como vimos, a segunda coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
Invertendo o sentido do vetor para usa-lo como positivo, assim teremos que
E assim terminamos as reações de apoio, vamos a determinação da força no tirante que é o nosso último passo.
Passo 5
Vamos ao último passo que consiste em definir o normal no nosso tirante, e pra isso iremos usar como auxilio a nossa rótula.
Agora é importante que você lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, por cima ou por baixo tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em C vindo por baixo, teremos que
E o ponto C será
Precisamos trocar o nosso tirante por forças normais na estrutura
E agora precisamos levar os carregamentos de baixo da rótula até a rótula
Fazendo o somatório de momentos na rótula teremos que
Logo a força no nosso tirante necessitou, nesse caso, das reações de apoio, mas, em alguns casos as reações de apoio não serão de suma importância na conta, com isso força no nosso tirante é uma força de tração de intensidade 65 KN
Resposta
Exercício Resolvido #6
Elaboração Própria
Determine o valor do Normal no Tirante do pórtico dado abaixo
Passo 1
Como já sabemos, precisamos fazer um passo a passo para sabermos como resolveremos o nosso problema, e o passo a passo é
- A primeira coisa que faremos é um balanceamento de incógnitas e equações e iremos confirmar se a nossa estrutura é isostática, sendo isostática iremos ao próximo passo do nosso problema.
- A segunda coisa que iremos fazer é o cálculo das reações de apoio do nosso problema
- Como o objetivo é determinar o normal no tirante, basta escolhermos com sabedoria um ponto para fazermos o somatório de momentos de forma que a força exercida na estrutura pelo tirante seja uma incógnita, e como já iremos ter determinado as reações de apoios no passo anterior, a força no tirante será a única incógnita, e dessa forma iremos determinar as forças no tirante.
Vamos aplicar o nosso passo a passo no exercício? Vamos lá.
Passo 2
Como vimos, o primeiro passo consiste em fazermos um balanceamento de incógnitas e equações, sabemos que primeiro devemos fazer um balanceamento de incógnitas, e para isso contabilizamos reações de apoios e o nosso tirante, dessa forma teremos que
Fazendo a contabilidade teremos
Ou seja, temos 4 incógnitas no nosso problema.
Passo 3
Vamos agora a contabilização do número de equações.
Sabemos que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Ou seja, podemos dizer que o número de equações do nosso problema é igual ao número de incógnitas, ou seja, temos um problema isostático, sendo assim, podemos ir para o próximo passo do nosso passo a passo, que é resolver as reações de apoio do nosso pórtico.
Passo 4
Como vimos, a segunda coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
Invertendo a direção para usarmos o valor positivo teremos que
E assim terminamos as reações de apoio, vamos a determinação da força no tirante que é o nosso último passo.
Passo 5
Vamos ao último passo que consiste em definir o normal no nosso tirante, e pra isso iremos usar como auxilio a nossa rótula.
Agora é importante que você lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, por cima ou por baixo tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em C vindo por baixo, teremos que
E o ponto C será
Precisamos trocar o nosso tirante por forças normais na estrutura
E agora precisamos levar os carregamentos de baixo da rótula até a rótula
Fazendo o somatório de momentos na rótula teremos que
Logo a força no nosso tirante necessitou, nesse caso, das reações de apoio, mas, em alguns casos as reações de apoio não serão de suma importância na conta, com isso força no nosso tirante é uma força de tração de intensidade 706,7 KN
Resposta
Exercício Resolvido #7
Elaboração Própria
Determine o valor do Normal no Tirante do pórtico dado abaixo
Passo 1
Como já sabemos, precisamos fazer um passo a passo para sabermos como resolveremos o nosso problema, e o passo a passo é
- A primeira coisa que faremos é um balanceamento de incógnitas e equações e iremos confirmar se a nossa estrutura é isostática, sendo isostática iremos ao próximo passo do nosso problema.
- A segunda coisa que iremos fazer é o cálculo das reações de apoio do nosso problema
- Como o objetivo é determinar o normal no tirante, basta escolhermos com sabedoria um ponto para fazermos o somatório de momentos de forma que a força exercida na estrutura pelo tirante seja uma incógnita, e como já iremos ter determinado as reações de apoios no passo anterior, a força no tirante será a única incógnita, e dessa forma iremos determinar as forças no tirante.
Vamos aplicar o nosso passo a passo no exercício? Vamos lá.
Passo 2
Como vimos, o primeiro passo consiste em fazermos um balanceamento de incógnitas e equações, sabemos que primeiro devemos fazer um balanceamento de incógnitas, e para isso contabilizamos reações de apoios e o nosso tirante, dessa forma teremos que
Fazendo a contabilidade teremos
Ou seja, temos 4 incógnitas no nosso problema.
Passo 3
Vamos agora a contabilização do número de equações.
Sabemos que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Ou seja, podemos dizer que o número de equações do nosso problema é igual ao número de incógnitas, ou seja, temos um problema isostático, sendo assim, podemos ir para o próximo passo do nosso passo a passo, que é resolver as reações de apoio do nosso pórtico.
Passo 4
Como vimos, a segunda coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
Invertendo a direção para usarmos o valor positivo teremos que
E assim terminamos as reações de apoio, vamos a determinação da força no tirante que é o nosso último passo.
Passo 5
Vamos ao último passo que consiste em definir o normal no nosso tirante, e pra isso iremos usar como auxilio a nossa rótula.
Agora é importante que você lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, por cima ou por baixo tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em C vindo por baixo, teremos que
E o ponto C será
Precisamos trocar o nosso tirante por forças normais na estrutura
E agora precisamos levar os carregamentos de baixo da rótula até a rótula
Fazendo o somatório de momentos na rótula teremos que
Logo a força no nosso tirante necessitou, nesse caso, das reações de apoio, mas, em alguns casos as reações de apoio não serão de suma importância na conta, com isso força no nosso tirante é uma força de tração de intensidade 182,5 KN