Colunas Especiais
Produzido por Marcelo AlvesTeoria
Motivação
Para fechar os tipos de coluna de destilação que podem aparecer no método Mc-Cabe Thiele gráfico, vamos ver como trabalhar com as colunas especiais. Lembrando que elas são tão especiais que geralmente aparecem nas provas
Coluna com arraste a vapor
Vapor de arraste somente utilizado quando na separação de soluções aquosas em que a água é o componente mais leve.
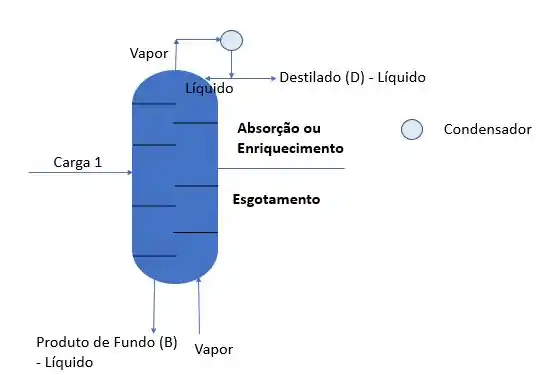
Nós vimos que as equações que fazem parte do balanço de massa dessa coluna são:
Lembrando que é a vazão de vapor d’água e que ela não aparece na equação por componente pois a concentração nessa corrente é nula. A única coisa que isso vai mudar para aplicar o método Mc-Cabe Thiele será a equação da ROSE. Já que a seção de absorção fica exatamente a mesma.
Para traçar essa reta no nosso Gráfico X-Y, temos que procurar dois pontos. O primeiro pode ser quando , pois nesse caso a composição de é , já que o vapor que cruza com o produto líquido de fundo é composto apenas de água.
O segundo ponto seria o ponto onde , localizado na diagonal. Para identificar esse ponto, vamos usar o balanço de massa da seção de esgotamento!
Como , podemos reorganizar e obter que:
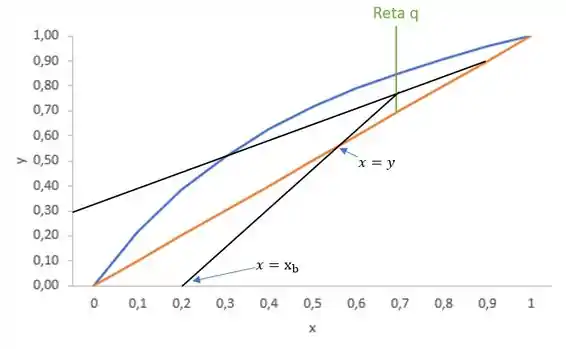
Bora marcar isso no gráfico? Considerando que a ROSA continua a mesma coisa :P
Coluna de Retificação ou Enriquecimento
As colunas de Enriquecimento são aquelas que possuem apenas a seção de absorção.
 Portanto, elas possuirão apenas a ROSA e a reta q. Além disso, a reta q e a composição do produto de fundo precisam coincidir em algum momento no gráfico, já que a carga e o produto de fundo se cruzam no fundo da coluna. E o outro ponto da reta ROSA será a composição do produto de topo.
Portanto, elas possuirão apenas a ROSA e a reta q. Além disso, a reta q e a composição do produto de fundo precisam coincidir em algum momento no gráfico, já que a carga e o produto de fundo se cruzam no fundo da coluna. E o outro ponto da reta ROSA será a composição do produto de topo.
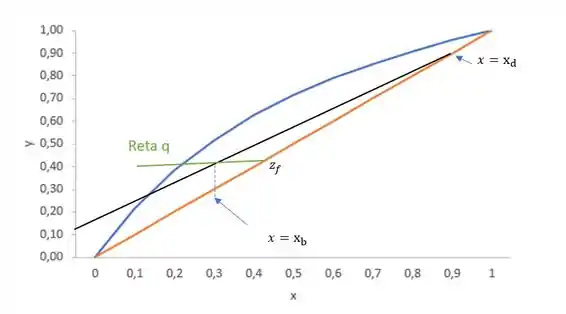
Então, assim é possível determinar a nossa ROSA pra traçar os estágios 😊
Coluna de Esgotamento
Por outro lado, a coluna de esgotamento só possui a seção de esgotamento! Então, para traçar sua ROSE é necessário traçar pelo fundo da coluna a partir da composição do produto de fundo.
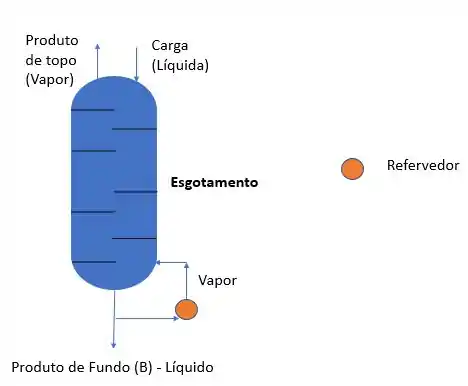
Nesse caso, temos a composição do produto de fundo e o outro ponto será dado pela interseção da reta q com o produto de topo que é um vapor.

Para traçar os estágios, é exatamente igual fazemos para os outros tipos de coluna, beleza?