Exercícios de Eficiência de O’ Cornell e Murphree - Lista de Exercícios Resolvida
Questão 1
Considere o diagrama abaixo. Indique qual tipo de eficiência é esta, considerando o modelo de Murphree.
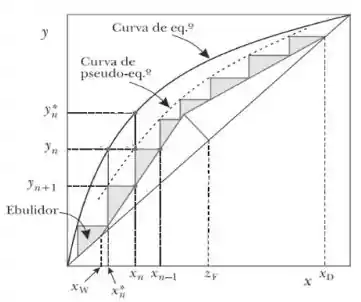
Questão 2
Considerando o diagrama abaixo. Calcule a diferença percentual entre o número de estágios teóricos e o número de estágios reais.
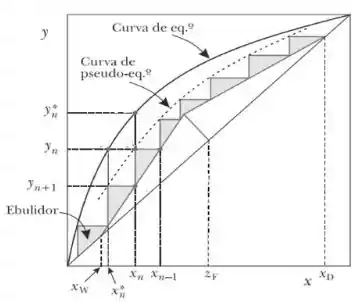
Questão 3
O gráfico abaixo representa uma simplificação da equação de O’connell, em que a eficiência global, , é dada por . Isso é válido de , onde , é a viscosidade e é a volatilidade.
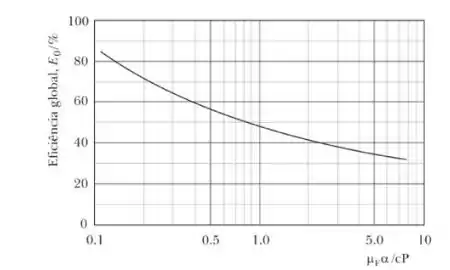
Sabendo que a eficiência global é de e a viscosidade é . Calcule o valor de .
Ver solução completaQuestão 4
A unidade de separação foi projetada para separar, a 1 atm, uma solução aquosa de etanol com de etanol. A vazão de carga é de , líquida subresfriada condensando um mol de vapor para cada quatro moles no prato de alimentação. Esta coluna está equipada com condensador parcial e usa vapor de arraste. O produto de topo deve ter de etanol e o produto de fundo . Deve-se assumir vazões molares constantes e considerar a Razão de Refluxo Operacional igual a 3. O vapor é vapor d’água puro saturado.
Nessas condições e considerando de eficiência, o diagrama de equilíbrio com os estágios operacionais possui o seguinte formato:
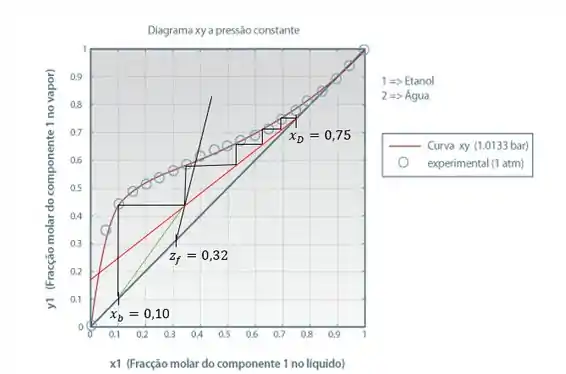
Considerando que a eficiência de Murphree na fase vapor é de apenas , determine o número de estágios necessários.
Ver solução completaQuestão 5
O gráfico abaixo representa uma simplificação da equação de O’connell, em que a eficiência global, , é dada por . Isso é válido de , onde , é a viscosidade e é a volatilidade.
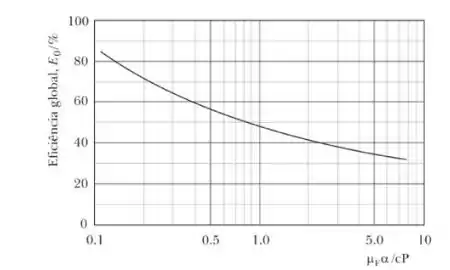
Considerando o gráfico acima e a equação fornecida, explique como a viscosidade pode influenciar a eficiência global.
Ver solução completaQuestão 6
A separação de água e ácido acético utilizando uma coluna de destilação, em determinadas condições, é especificada pela imagem a seguir:
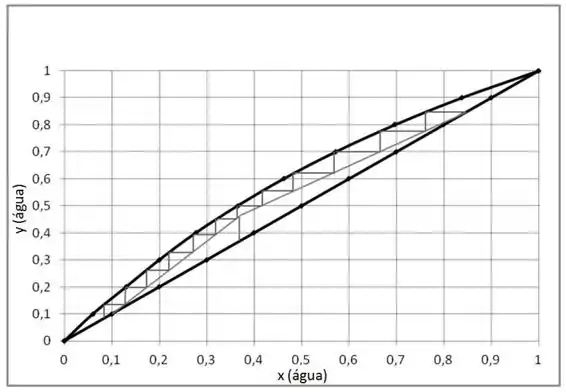
Essa coluna de destilação considera uma eficiência de . Indique o número de estágios teóricos e reais, considerando que a coluna opera com uma eficiência de .
Ver solução completa