Determine o valor do Normal no Tirante do pórtico dado abaixo
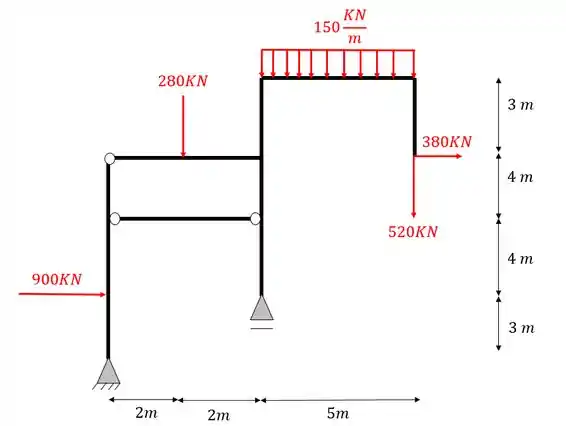
Passo 1
Como já sabemos, precisamos fazer um passo a passo para sabermos como resolveremos o nosso problema, e o passo a passo é
- A primeira coisa que faremos é um balanceamento de incógnitas e equações e iremos confirmar se a nossa estrutura é isostática, sendo isostática iremos ao próximo passo do nosso problema.
- A segunda coisa que iremos fazer é o cálculo das reações de apoio do nosso problema
- Como o objetivo é determinar o normal no tirante, basta escolhermos com sabedoria um ponto para fazermos o somatório de momentos de forma que a força exercida na estrutura pelo tirante seja uma incógnita, e como já iremos ter determinado as reações de apoios no passo anterior, a força no tirante será a única incógnita, e dessa forma iremos determinar as forças no tirante.
Vamos aplicar o nosso passo a passo no exercício? Vamos lá.
Passo 2
Como vimos, o primeiro passo consiste em fazermos um balanceamento de incógnitas e equações, sabemos que primeiro devemos fazer um balanceamento de incógnitas, e para isso contabilizamos reações de apoios e o nosso tirante, dessa forma teremos que
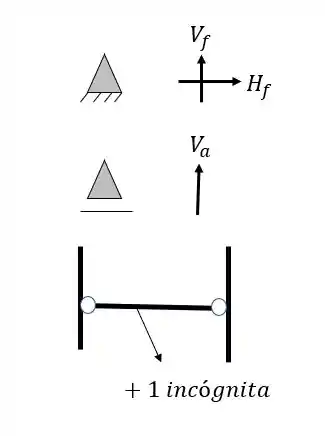
Fazendo a contabilidade teremos
Ou seja, temos 4 incógnitas no nosso problema.
Passo 3
Vamos agora a contabilização do número de equações.
Sabemos que temos 3 equações de equilíbrio
E que o nosso pórtico apresenta uma rótula
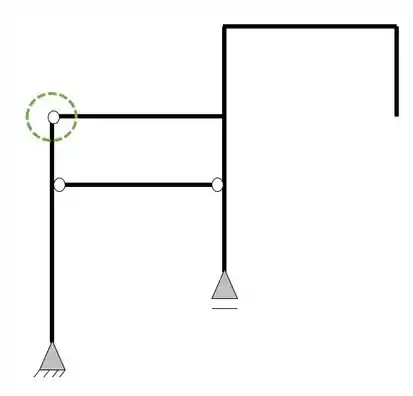
Como podemos ver, temos duas barras nessa rótula, logo, teremos o seguinte
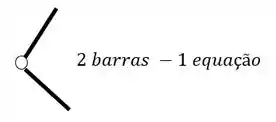
Fazendo a contabilidade, teremos um total de 4 equações, 3 de equilíbrio e 1 da rótula.
Ou seja, podemos dizer que o número de equações do nosso problema é igual ao número de incógnitas, ou seja, temos um problema isostático, sendo assim, podemos ir para o próximo passo do nosso passo a passo, que é resolver as reações de apoio do nosso pórtico.
Passo 4
Como vimos, a segunda coisa que devemos fazer é determinar as reações de apoio, para isso, primeiro iremos trocar os apoios por vetores reações de apoio, como indica a figura abaixo.
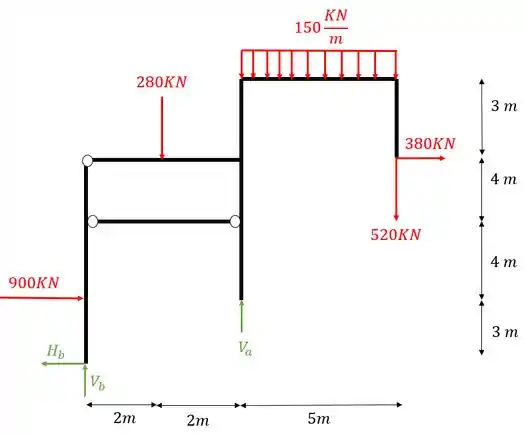
Agora que já temos os vetores e medidas, vamos fazer o equilíbrio de equações
E sabemos que quando da negativo, podemos, nesse caso, inverter o nosso vetor para podermos usá-lo com sinal positivo.
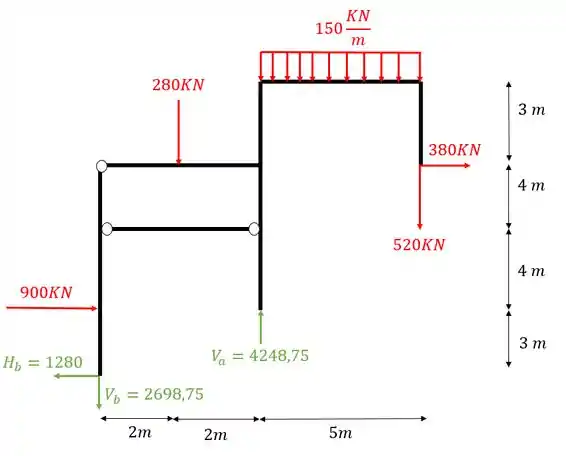
E assim terminamos as reações de apoio, vamos a determinação da força no tirante que é o nosso último passo.
Passo 5
Vamos ao último passo que consiste em definir o normal no nosso tirante, e pra isso iremos usar como auxilio a nossa rótula.
Agora é importante que você lembre-se que as rótulas também fornecem equações, e nesse caso, a equação que ela fornece é de que o somatório de momentos fletores nela, vindo pela esquerda ou pela direita, por cima ou por baixo tem que ser, obrigatoriamente, zero, com isso, se fizermos o somatório de momentos fletores em C vindo por baixo, teremos que
E o ponto C será
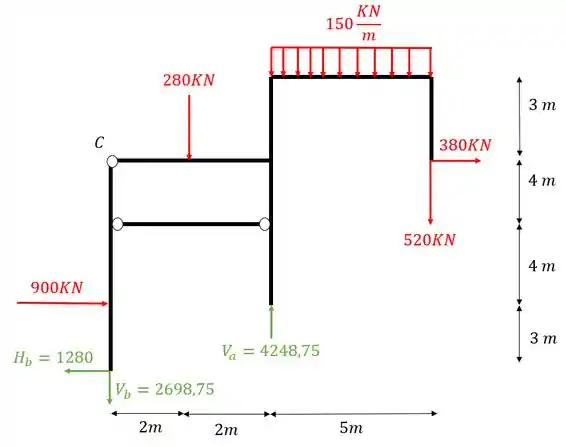
Precisamos trocar o nosso tirante por forças normais na estrutura
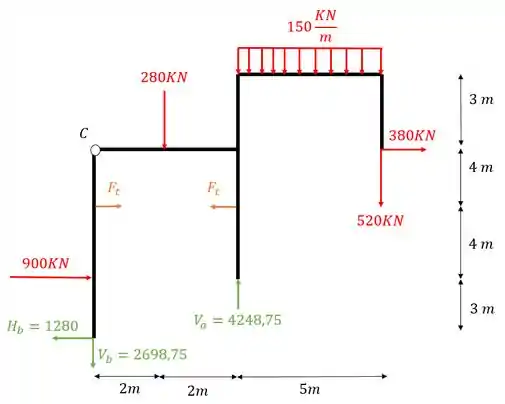
E agora precisamos levar os carregamentos de baixo da rótula até a rótula
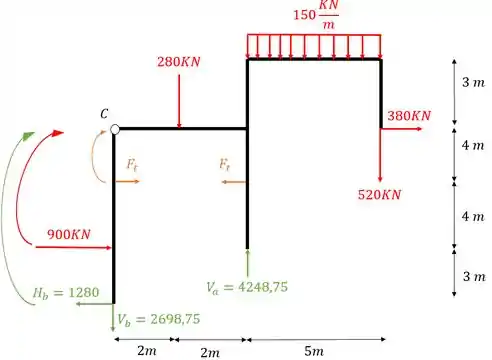
Fazendo o somatório de momentos na rótula teremos que
Logo a força no nosso tirante necessitou, nesse caso, das reações de apoio, mas, em alguns casos as reações de apoio não serão de suma importância na conta, com isso força no nosso tirante é uma força de tração de intensidade 1720 KN