Distribuição de Frequência
Produzido por Jorge Alberto NascimentoTeoria
Fala aí! Bora aprender TUDO de distribuição de frequência com o RespondeAí?!
Vamo que vamo então! Olha só esse vídeo iradaço que o RespondeAí preparou especialmente pra você! 👇 🧡
Para conferir a parte 2 desse vídeo você pode clicar aqui!
Ou continuar comigo para um resuminho em texto! 👇 😉
Pra começar com tudo, vamos logo para um exemplo! Digamos que um nutricionista de uma equipe com
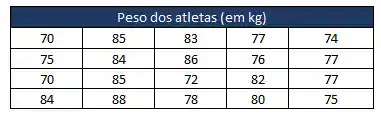
Nós veremos aqui que podemos analisar os dados de duas formas: de uma forma individual e agrupando os dados.
Para facilitar esse agrupamento, vamos construir nossa tabela Rol, que nada mais é do que arranjar os dados em ordem crescente.
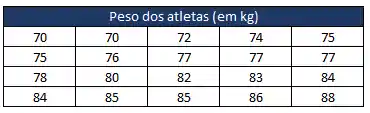
Só em fazer isso, já podemos observar:
- O menor e o maior valor:
e - O valor que mais aparece:
- A amplitude da variação dos pesos :
Beleza, mas a gente pode fazer uma tabela ainda mais visual, certo?!
Tabela de Distribuição de Frequência
Uma forma mais resumida de mostrar os dados do Rol é apresentar quantas vezes cada peso aparece na tabela do Rol. Dessa forma, construímos nossa tabela de distribuição de frequência.
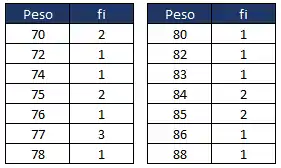
O número de ocorrências de um determinado valor recebe o nome de frequência absoluta
Essa tabela de distribuição de frequências acima considera dados não agrupados.
Frequências Relativa e Acumulada
Agora veremos outros tipos de frequências que existem. Utilizaremos elas para calcular as medidas de dispersão mais à frente.
A gente viu que frequência absoluta é a quantidade de ocorrências de um valor, né?! Além dessa, temos:
- Frequência relativa
será a frequência absoluta de um valor dividido pelo total de valores.
Voltando ao exemplo, se quisermos calcular a frequência relativa doteremos: - Frequência acumulada
é o total acumulado (soma) de todas as frequências absolutas anteriores até a frequência absoluta do valor atual. No nosso exemplo, se quisermos calcular a frequência acumulada do valor
teremos - Frequência acumulada relativa
é você ir dividindo o valor da frequência acumulada pelo total de valores. Voltando ao exemplo, se quisermos calcular a frequência acumulada relativa do
, teremos:
Conselho: tomar muito cuidado pra não confundir esses f’s todos 🤣🤣🤣
Organizando essas informações em tabela, para o nosso exemplo:
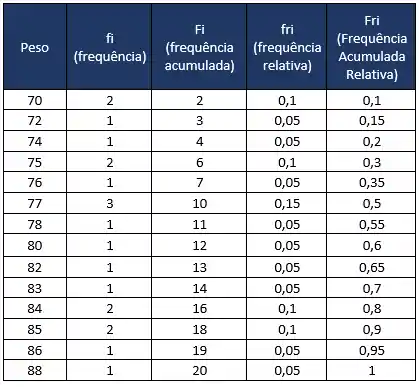
Um tabelão, né?! Ahahaha
Você pode estar se perguntando se tem uma forma de resumir esses dados sem precisar levar em conta os valores individuais...
Então eu te respondo: Tem sim!!!!!!
Podemos agrupar esses dados!! Mas, como faremos isso?
Tabela de Distribuição de Frequência com Dados Agrupados
O que a gente vai fazer agora é ver dois jeitos de agrupar os nossos dados, e depois construir uma tabela com a distribuição de frequências, com os dados já agrupados!
Como faremos isso? Iremos agrupar os dados em classes... de
Calma, não é tão aleatório assim!!
Regra de Sturges
Existe uma regrinha que vai nos ajudar a determinar o número de intervalos que são necessários para representar graficamente um conjunto de dados estatísticos adequado pra cada situação!! Se chama Regra de Sturges.
A fórmula dessa regra tem essa carinha:
Onde
No nosso exemplo, teríamos:
Regra da Raíz
Existe outra regrinha que pode nos ajudar nessa missão de determinar o número de classes! O nome dela é Regra da Raíz!! A fórmula é essa:
Onde
Reparou que os valores de
Vai depender de como seu professor cobra isso, ou vai ser dito na questão, ou até mesmo se você quer ser mais minucioso e dividir em mais classes ou não.
Aqui eu vou usar a regra de Sturges! Dessa forma, teremos mais classes e será melhor para visualizar a distribuição dos dados.
Agora podemos calcular o tamanho do intervalos de cada classe
Onde
Assim:
Dessa forma, agrupando os dados de
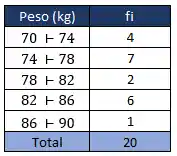
Todos aqueles tipos de frequências que vimos para dados não agrupados podem ser expandidos pra dados agrupados também, quando temos as classes. Ao invés de termos a frequência de um valor, a gente tem a frequência de uma classe. Mas as fórmulas e o pensamento continua o mesmo.
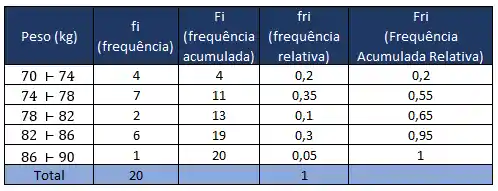
Com todos esses valores em mãos, podemos montar nossa tabela da distribuição de frequência final:
Agora bora praticar com exercícios?!
Tabela de Distribuição de Frequência
Tabela de Distribuição de Frequência com Dados Agrupados
Exercícios Resolvidos
Exercício Resolvido #1
UERJ-LISTA 1- PROF FABIANO-4
Os dados seguintes representam 20 observações relativas ao índice pluviométrico em determinado município. Construir a distribuição de frequência para dados não grupados.
Passo 1
Para construir a distribuição de frequência para esses dados não grupados precisamos construir uma tabela com os valores de em ordem crescente:

Beleza?!
Passo 2
Vamos lá! Vamos calcular a frequência absoluta de cada valor que é quantas vezes cada um aparece:
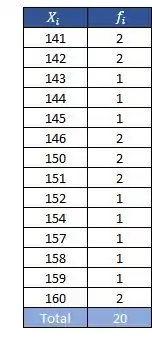
Passo 3
Agora vamos calcular a nossa frequência acumulada
Só ir somando as anteriores;
Por exemplo,
Agora é só repetir o processo para achar os outros valores:
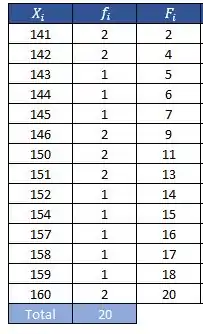
Passo 4
Agora vamos calcular a nossa frequência relativa
Para isso, vamos dividir pelo total de valores que no caso são 20;
Quando tivermos então . Da mesma forma, quando então .
Assim,
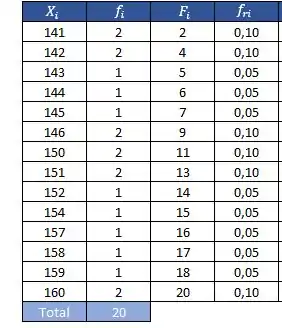
Passo 5
Agora vamos construir nossa frequência relativa acumulada
Basta dividir pelo total de valores (20):
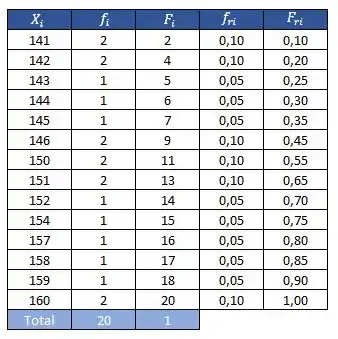
Resposta
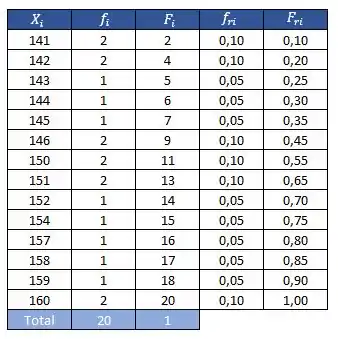
Exercício Resolvido #2
Elaboração Própria
Considere os seguintes dados os percentuais de lucros mensais de uma corretora de imóveis:
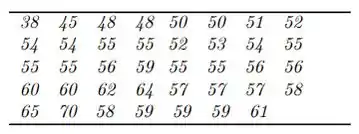
Construa um a tabela de diagrama de frequência com dados agrupados usando a regra da raiz.
Passo 1
Temos aí um total de dados. Então o número de classes que temos que ter na nossa tabela, pela regra da raiz, é:
A amplitude dos nossos dados é o dado de maior valor menor o de menor valor, ou seja:
E o intervalo de cada classe vai ser dado por:
Nossos dados em ordem crescente:

Agora agrupando esses dados de em , começando no primeiro dado que é o o e contando as quantidade de elementos dentro de cada classe (cada agrupamento) temos...
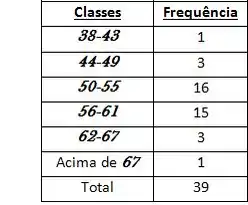
Resposta
Exercício Resolvido #3
MPE BA – FGV 2017
A distribuição de frequências do número de apreensões de valores (em milhões R$) realizadas pela Polícia Federal, em determinado período, é conforme a seguir:
Assim sendo, é correto afirmar que:
A) o último Decil está na penúltima classe;
B) a mediana da distribuição está na 2ª classe;
C) a média da distribuição está na 3ª classe;
D) a moda exata da distribuição está na 1ª classe;
E) a distribuição é assimétrica à esquerda.
Passo 1
Somando todas as frequências temos um total de:
Dividindo isso aí por dois vemos que a mediana está:
Na posição . E essa posição é acontece justamente ali na 2ª classe, certo? Já que a frequência acumulada da 2ª classe é , e a primeira classe tem itens, todos os dados entre e vão pertencer a 2ª classe!
Então a resposta é a letra B).
Resposta
Letra B)
Exercício Resolvido #4
Elaboração Própria
Considere os seguintes dados os percentuais de lucros mensais de uma corretora de imóveis:
Construa um a tabela de diagrama de frequência com dados agrupados usando a regra da raiz.
Passo 1
Temos aí um total de dados. Então o número de classes que temos que ter na nossa tabela, pela regra da raiz, é:
A amplitude dos nossos dados é o dado de maior valor menor o de menor valor, ou seja:
E o intervalo de cada classe vai ser dado por:
Nossos dados em ordem crescente:
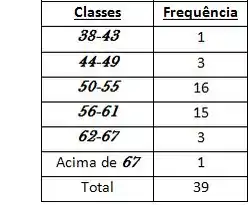
Agora agrupando esses dados de em , começando no primeiro dado que é o o e contando as quantidade de elementos dentro de cada classe (cada agrupamento) temos...
Resposta
Exercício Resolvido #5
As tabelas na parte inferior correspondem às notas dos alunos matriculados na disciplina de Estatística. Usando os dados apresentados, calcule os quartis principais e a DIQ.
Passo 1
Temos um total de dados, então .
Primeiro vamos verificar as posições dos quartis:
Passo 2
Com as posições calculadas, temos que procurar os dados que ocupam a posição na segunda tabela, nos baseando pelas frequências acumuladas.
Para o primeiro quartil, queremos a posição 15. A classe que acumula 15 frequências é a . Para calcular o quartil dentro de uma classe, usamos a fórmula:
Onde:
Então:
Passo 3
Agora para o segundo quartil, que está na posição 30. Essa posição se encontra dentro da classe . Aplicando a fórmula para o cálculo do quartil:
E agora o terceiro quartil, que está na posição 45, dentro da classe :
Passo 4
Calculando nossa DIQ: