Medidas de Centralidade e Dispersão para Dados Agrupados
Produzido por Jorge Alberto NascimentoTeoria
Introdução
Fala Aí!! Digamos que um nutricionista de uma equipe de 20 atletas dividiu a equipe em grupos para saber qual tipo de dieta cada grupo deverá fazer de acordo com o peso de cada um. Ao montar a tabela de distribuição de frequências para dados agrupados, ficamos com essa carinha:
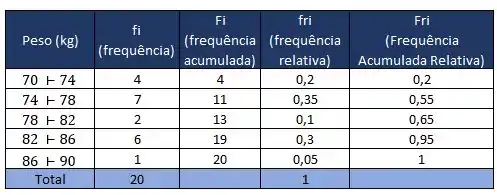
E se quisermos calcular as medidas de centralidade e dispersão utilizados para representar esses dados?
HOJE É O SEU DIA DE SORTE, POIS É O QUE VAMOS VER AQUI!!!!

Tu lembra que Média, Moda, Mediana, Variância, Desvio Padrão é tuudo fórmulinhas, né?! Então não temos como fugir muito disso para dados agrupados hahahaha
Medidas de Centralidade
Média aritmética
Para dados agrupados usaremos:
Nesse caso é o ponto médio da classe. Por exemplo se a classe vai de 4 até 10,
No nosso exemplo:
Show de bola?
Mediana
Para dados agrupados usaremos o seguinte passo-a-passo:
- Calcular a posição , idenpendente se for par ou ímpar;
- Identificar qual classe contém a mediana (onde está a posição );
- Usar a fórmula:
limite inferior da classe que contém a mediana.
frequência acumulada anterior à classe que contém a mediana.
frequência dessa classe.
amplitude da classe
Voltando pro nosso exemplo, temos primeiro que identificar a classe da mediana.
Para isso, calculamos o valor de que será .
Agora, olhando para os valores de procuramos em qual classe estará o valor 10. Percebemos que está na classe , concorda?
Ai usamos a fórmula:
Beleza?!
Quartis primeiro e terceiro
Lembrando que a mediana também é o segundo quartil, podemos aproveitar e fazer logo um paralelo com o primeiro e o terceiro quartil. Eles vão ser dados por:
limite inferior da classe que contém o quartil.
frequência acumulada anterior a classe que contém o quartil.
frequência dessa classe.
amplitude da classe
Vamos calcular no nosso exemplo. Se você reparar, a classe que contém o quartil é a classe . Assim,
Beleza?!
Moda
Quando os dados estão agrupados, a moda corresponde a classe com frequência simples mais alta e o valor da moda é tomado como sendo o valor médio dessa classe.
limite inferior da classe modal
frequência da classe modal menos a da classe anterior
frequência da classe modal menos a da classe posterior
amplitude da classe
Para calcular a moda no nosso exemplo temos primeiro que achar a classe modal que é a classe com a maior frequência absoluta. No caso é a classe que tem , beleza?!
Aí usamos a fórmula:
De boa até aqui?! Então vamos continuar!
Também podemos calcular as medidas de dispersão, que indicam o espalhamento dos valores da amostra em torno da medida de centralidade.

Para dados grupados em classes, vamos usar essas a fórmulas que são bem parecidas com o que estamos acostumados:
Variância amostral
Lembrando que ainda é o termo central da classe.
Assim, ficamos com:
Logo,
Beleza?!
Como temos a variância, conseguimos agora encontrar o desvio padrão amostral.
Desvio padrão amostral
Show de bola?! E pra fechar com chave de ouro conseguimos calcular o coeficiente de variação amostral.
Coeficiente de variação amostral
Fórmula, fórmula, fórmula, não desista! Perceba que você já conhecia esses carinhas aí, e as fórmulas continuaram quase as mesmas.
Vamos exercitar que você vai ficar craque nisso!
Exercícios Resolvidos
Exercício Resolvido #1
UERJ-LISTA 1- PROF FABIANO-8
Considerando os dados abaixo:
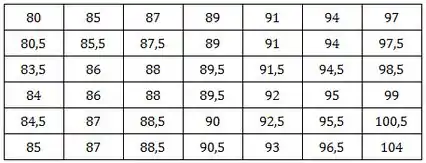
- Construa a distribuição de frequência para dados grupados (utilizando Sturges);
- Encontre a amplitude total;
- Calcule a média;
- Calcule a mediana;
- Calcule a moda;
- Calcule a variância;
- Calcule o desvio padrão;
- Calcule o coeficiente de variação.
Passo 1
(a)
Aqui nós montaremos uma tabelinha de distribuição de frequência assim como fazíamos para os dados, a diferença é que aqui agruparemos os dados para montar!
Então, a primeira coisa que faremos como queremos dados agrupados, é dividir os valores em classes.
O exercício pede pra usarmos a regra da Sturges. Como vimos lá na teoria, a fórmula para essa regra é:
Onde é o número de elementos da nossa amostra e a quantidade de classe que vamos ter! Se a gente tem 42 valores na amostra:
Arredondando isso aí, vamos ter então 6 classes.
Passo 2
(b) Agora precisamos calcular a amplitude da nossa amostra.
Reparem que a nossa tabela já tá em ordem crescente! A diferença aqui é que tá crescendo “pra baixo”, no sentido das colunas, e não das linhas.
Então podemos ver de cara que o maior valor que temos é 104 e o menor é 80.
A amplitude total da amostra é então:
Com isso, cada classe vai ter uma amplitude igual a:
Ou seja vamos ter classes de 4 em 4, começando por 80.
Passo 3
Para construir a distribuição de frequência vamos montar uma tabela com as seguintes colunas:
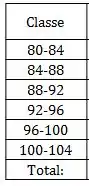
Vamos ver como fica para a nossa primeira classe, que vai começar em e como , vai terminar em . Nossos valores entre e são:
Lembrem que nunca contamos o valor que “fecha” o intervalo, no nosso caso o .
Vamos calcular as informações dessa primeira classe então. Começando pelo valor médio . Se a classe vai de a , o valor médio é:
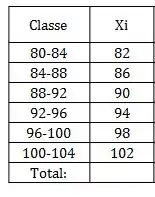
Agora a frequência absoluta da classe, ou seja, quantos elementos temos dentro dela. Por exemplo,
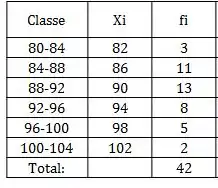
Só ir somando as anteriores;
No primeiro caso
Por quê? Porque essa é nossa primeira classe, então não temos nenhuma frequência acumulada para somar a ela, por que não há classes antes dela!
No caso
E vamos seguir esse mesmo processo pro restante! Ficaremos com
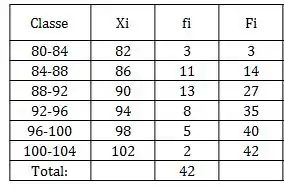
Que é dividir pelo total de valores que no caso são 42;
Por exemplo, na primeira classe a frequência relativa vai ficar:
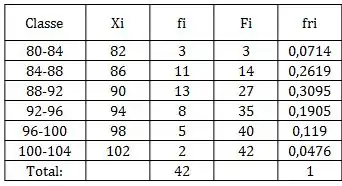
Que é dividir pelo total de valores (42). Para a primeira classe, teriamos
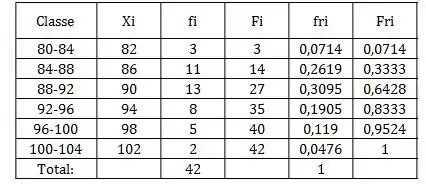
Passo 4
Repetindo esse passo a passo para todas as classes, ficaria algo assim:
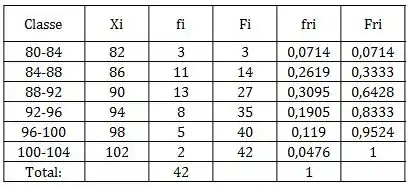
Passo 5
(c)
Para dados grupados calculamos a média usando:
Passo 6
(d)
Pra calcular a mediana, temos primeiro que identificar a classe da mediana.
Para isso calculamos o valor de que será .
Agora, olhando para os valores de procuramos em qual classe estará o valor 21. Percebemos que a classe tem . Como queremos 21 não usaremos essa e sim a seguinte.
No nosso caso a classe da mediana será .
Ai usamos a fórmula:
Onde
limite inferior da classe que contém a mediana.
frequência acumulada anterior à classe que contém a mediana.
frequência dessa classe.
amplitude da classe
Assim,
Passo 7
(e)
Para calcular a moda, temos primeiro que achar a classe modal que é a classe com a maior frequência absoluta.
No casso é a classe que tem .
Aí usamos a fórmula:
Onde
limite inferior da classe modal
frequência da classe modal menos a da classe anterior
frequência da classe modal menos a da classe posterior
amplitude da classe
Passo 8
(f)
Para a variância vamos usar a fórmula:
Passo 9
(g)
Desvio padrão:
Passo 10
(h)
Coef. De variação:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
PUCRIO-P1-2011.2
Observe a seguinte estatística descritiva referente a uma determinada amostra:
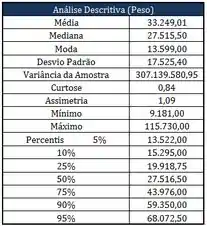
Com relação à estatística descritiva acima, responda as perguntas abaixo:
- Qual o coeficiente de variação da amostra?
- Qual a amplitude máxima da amostra?
- Assimetria positiva indica que existem mais valores altos do que baixos? Sim ou não?
- O que o coeficiente de curtose desta amostra nos permite dizer com relação a uma Normal?
- O que o percentil de desta amostra nos permite dizer?
- Qual é o valor que se repete mais vezes da amostra?
- Na tabela abaixo, temos o diagrama de frequência de uma de elementos onde: os intervalos são iguais; é o ponto médio de cada classe (intervalo); frequência absoluta simples; frequência cumulada. Preencher os espaços vazios do diagrama de frequência.
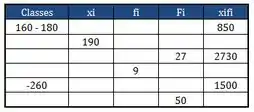
Passo 1
(a)
Coeficiente de variação é aquela fórmula, desvio padrão dividido pela média. Tudo isso tá na tabela, só dividir.
Passo 2
(b)
Amplitude máxima é o maior valor menos o menor valor, tranquilo, tudo na tabela de novo.
Passo 3
(c)
Não, assimetria positiva quer dizer que a média é maior que a mediana, isso significa que temos mais valores baixos do que altos.
Passo 4
(d)
Nossa curtose é positiva, o que simboliza uma curva leptocúrtica, aquela com o pico mais alto, lembra? Tem maior curtose que a Normal, comparativamente.
Passo 5
(e)
Nos permite dizer que dos valores da amostra estão abaixo de .
Passo 6
(f)
O valor que mais se repete é a nossa moda, que pode ser vista na tabela.
Passo 7
(g)
Vamos devagar, completar as classes é izi, as classes são todas do mesmo tamanho.
Se a primeira classe vai de , então todas as classes tem amplitude de , só ir completando.
Com isso, completar os também é tranquilão, são os pontos do meio da classe.
Na classe que já ali, , teremos:
Completando esses dois ficamos assim:
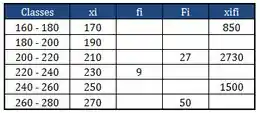
Passo 8
Agora podemos pensar que conhecemos alguns e alguns , então podemos tirar os facilmente.
Do mesmo jeito, conhecemos o e o de uma classe e podemos conhecer o só multiplicar.
Ficaria assim:
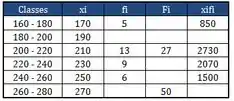
Passo 9
Agora vamos lá, na coluna do eu vou somando os valores de das classes anteriores, concorda?
Então por exemplo, ali a partir do , posso somar e depois ... descobrindo o das classes e , respectivamente.
Hmmm, se o próximo é , consigo descobrir o da última classe que estava faltando também, cert?
E com esse descubro o , multiplicando:
Fiz muita coisa, vamos ver como ficou...
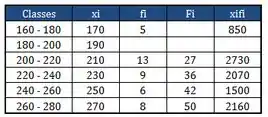
Passo 10
Falta um da coluna que é de boas, só você lembrar que o somatório dessa coluna tem que ser , que é o total de elementos.
E então calculamos:
O primeiro é igual ao , concorda? Não tem mais nada pra acumular, então o segundo será , que é
Finalmente chegamos à tabela completa:
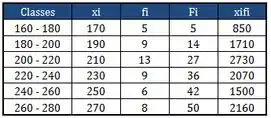
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
MPE BA – FGV 2017
A distribuição de frequências do número de apreensões de valores (em milhões R$) realizadas pela Polícia Federal, em determinado período, é conforme a seguir:
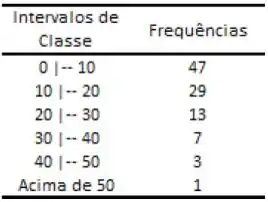
Assim sendo, é correto afirmar que:
A) o último Decil está na penúltima classe;
B) a mediana da distribuição está na 2ª classe;
C) a média da distribuição está na 3ª classe;
D) a distribuição é assimétrica à esquerda.
Passo 1
Nessa questão, vamos avaliar cada um dos itens e ver qual é o verdadeiro e quais são falsos!
A letra A), diz que o último Decil está na penúltima classe. Vamos encontrar então quem é o nosso último Decil.
O Decil nada mais é do que o elemento que divide os nossos dados em grupos de , por isso, o primeiro Decil é o dado que representa o valor na posição de 10%, o segundo Decil o valor na posição de 20%, o quinto Decil, por exemplo, é o valor na posição de 50% que é o mesmo valor que a mediana!Nós temos um total de nove decis, e o último decil é o elemento que representaria a posição de 90%.
Somando todos as frequências, temos um total de:
Opa! Aí tá fácil né, como temos 100 dados, o último decil vai ser exatamente o dado da posição 90.
Fazendo a frequência acumulada por classes, vemos que:
A classe 1 vai do dado 1 até o dado 47.
A classe 2 vai do dado 48 até o dado ().
A classe 3 vai do dado 77 até o dado ().
Opa, o nosso último decil então está na classe 3, que não é a penúltima classe, logo essa está errada.
Passo 2
A letra b), diz que a mediana se encontra na segunda classe.
A mediana acontece na posição de que nesse caso aonde temos 100 dados, será o dado de número .
E essa posição acontece justamente ali na 2ª classe, certo? Já que a frequência acumulada da 2ª classe é , e a primeira classe tem itens, todos os dados entre e vão pertencer a 2ª classe!
Então a resposta é a letra B).
Passo 3
A letra c), diz que a média da distribuição está na terceira classe.
Média aritmética
Para dados agrupados usaremos:
Ou seja,
E podemos ver que a segunda classe tem um intervalo de valores entre e , por isso a média está na segunda classe e não na terceira, por isso está errada.
Passo 4
Na letra D), diz que a distribuição é assimétrica a esquerda.
Isso vai ocorrer quando a moda for maior que a mediana.
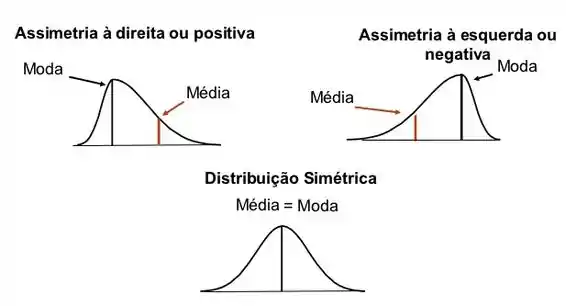
(Se a moda for igual a mediana, a distribuição é simétrica e se for menor é assimétrica a direita.)
Vamos encontrar aonde está nossa moda, então!
Temos que a classe com maior frequência é a primeira classe, logo a moda ocorre nessa classe e por isso é menor que a média (que ocorre na segunda classe).
Sendo assim, essa é uma distribuição assimétrica à direita e não à esquerda e essa alternativa D) está errada.
Por fim, a única alternativa correta é a letra B).
Resposta
Letra B)
Exercício Resolvido #4
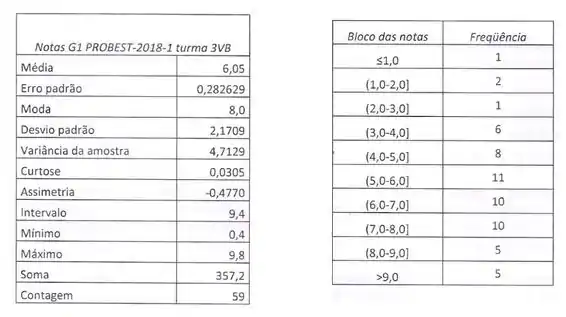
As tabelas na parte inferior correspondem às notas dos alunos matriculados na disciplina de Estatística. Usando os dados apresentados, calcule os quartis principais e a DIQ.
Passo 1
Temos um total de dados, então .
Primeiro vamos verificar as posições dos quartis:
Passo 2
Com as posições calculadas, temos que procurar os dados que ocupam a posição na segunda tabela, nos baseando pelas frequências acumuladas.
Para o primeiro quartil, queremos a posição 15. A classe que acumula 15 frequências é a . Para calcular o quartil dentro de uma classe, usamos a fórmula:
Onde:
Então:
Passo 3
Agora para o segundo quartil, que está na posição 30. Essa posição se encontra dentro da classe . Aplicando a fórmula para o cálculo do quartil:
E agora o terceiro quartil, que está na posição 45, dentro da classe :
Passo 4
Calculando nossa DIQ: