Gráfico de Barras, Setores & Histograma
Teoria
Fala Aíí!! Digamos que a gente trabalhe numa corretora de imóveis e para nos auxiliar a saber quais imóveis temos à venda montamos a tabelinha abaixo:
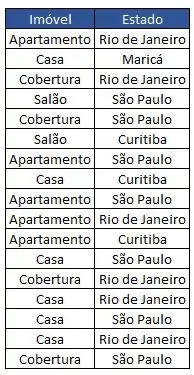
Para facilitar nossa vida, organizamos essa tabela de acordo com a quantidade (frequência) dos tipos de imóveis:
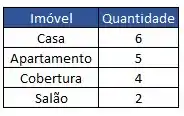
Beleza, temos a tabelinha com os nossos dados... mas será que é possível representar de uma forma mais atrativa esses dados? É possível sim!! Veremos aqui que podemos fazer isso utilizando os diversos tipos de gráficos que existem!
Gráfico de Barras e Setores
Uma forma muuito utilizada para resumir os dados de uma forma mais atrativa é utilizando o Gráfico de Barras!
Gráfico de Barras
A ideia do gráfico de barras é podermos analisar tanto as frequências relativas, de cada variável que estamos analisando, quanto a frequência absoluta. No nosso exemplo, teremos:
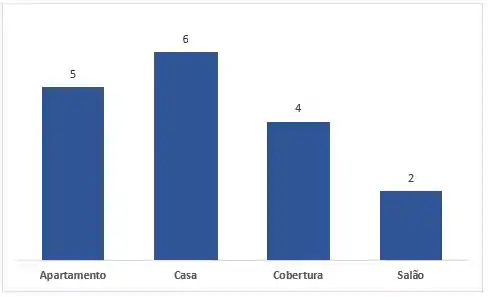
Com esse exemplo, podemos ver que o tipo de imóvel que mais se encontra à venda são as casas, em seguida coberturas, e por aí vai...
Gráfico de Setores (ou gráfico de pizza, para os mais íntimos)
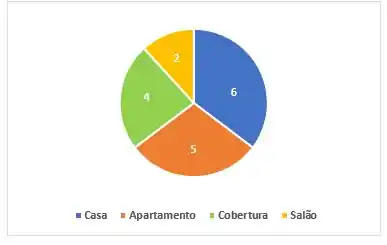
Aqui a gente também está interessado nas frequências relativas, porém colocamos nossos dados dentro uma pizza! Haha
Cada variável vai representar uma fatia, sendo que o tamanho é proporcional à frequência.
Também colocamos cada fatia de uma cor, para que, com uma legenda, possamos saber qual representa cada variável.
Tranquilo até aqui?!
Histograma
Para falarmos de histograma, vamos mudar um pouco o nosso exemplo, pode ser?
Considere agora a tabela abaixo com as faixas de peso, em Kg, para 20 indíviduos fictícios.
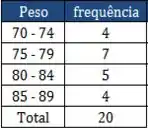
Histograma não tem mistério, ele é bem parecido com o tradicional gráfico de barras. Nele, representamos os intervalos de classe em um eixo e as frequências absolutas de cada intervalo no outro eixo.
A diferença entre o histograma e o gráfico de barras é que no histograma é sempre para intervalo de valores enquanto que o gráfico de barras é para um determinado valor ou parâmetro.
No nosso caso, ficaria assim...
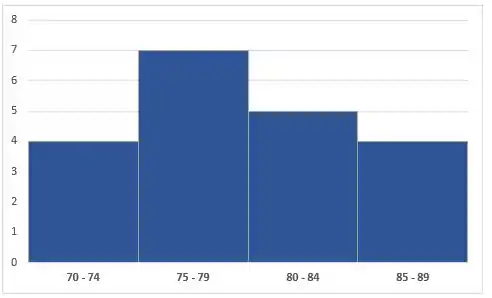
Outra coisa importante, é que temos dois tipos de histograma: vertical e horizontal.
No histograma vertical, os intervalos a gente marca no eixo horizontal e a frequência no eixo vertical. Se você fizer o contrário, vai ter o histograma horizontal. Beleza? No nosso exemplo, temos um histograma vertical, um histograma horizontal seria desse tipo:
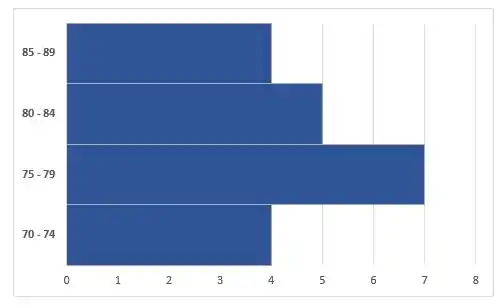
Polígono de Frequência
Se histograma não tem mistério, polígono de frequência têm menos ainda, confia em mim!
Um polígono de freqüência é uma representação gráfica de uma tabela de freqüência, que pode ser obtida através do histograma.
Basta você ligar os pontos médios de cada classe. E adicionar uma classe antes e outra depois com frequência zero pra fechar o polígono.
No nosso caso, ficaria assim...
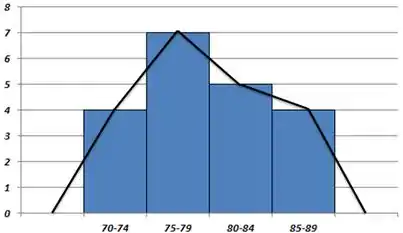
Diagrama de Pareto
Fazer um Diagrama de Pareto também não é nenhum absurdo... Olha só
O passo a passo é o seguinte:
- Calcular as frequências relativas de cada classe
- No eixo colocar as frequências absolutas, igual a gente fez no histograma.
- No eixo temos que colocar em ordem decrescente, primeiro o intervalo que tem maior frequência absoluta, depois o segundo maior e assim por diante.
- Pra finalizar, a gente tem que adicionar outro eixo do lado direito com as frequências relativas acumuladas de cada intervalo e ligar os pontos (com retas).
No nosso exemplo ia ficar mais ou menos assim a tabela de frequências modificada.
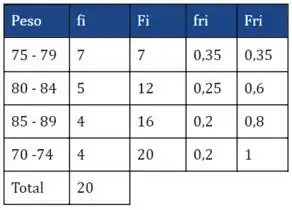
Seguindo o passo a passo que eu falei ali, o diagrama de pareto seria:
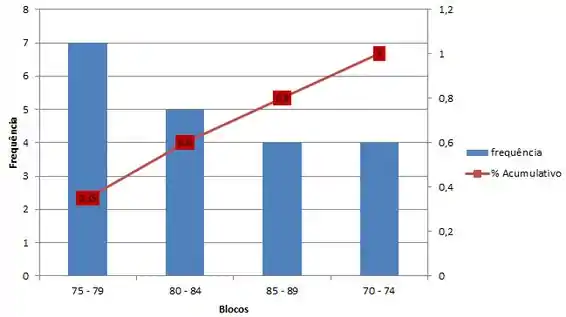
Se você notar, a gente poderia também representar a frequência relativa acumulada (% acumulativo) no histograma. Beleza?
Pra ficar mais claro, vou colocar aqui embaixo pra você ver.
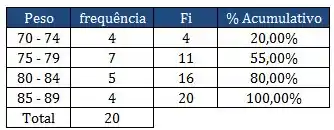
Assim, teremos
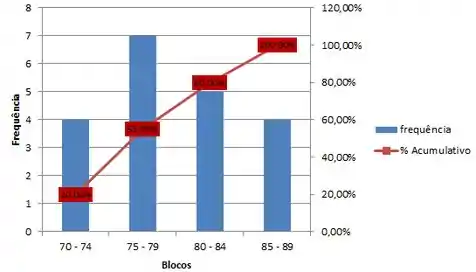
Agora pra a gente ter certeza que estamos craques nesses gráficos, bora praticar!?
Histograma
Polígono de Frequência
Diagrama de Pareto
Exercícios Resolvidos
Exercício Resolvido #1
UFJF- Probabilidade e Estatística – Lista – 2012 – Questão 01
Considere os dados de Sexo e Raça para os dados abaixo: 
a) Construa a tabela de frequência para cada uma das variáveis.
b) Faça os gráficos de barras e de setores (pizza) para cada uma das variáveis.
Passo 1
a) Construa a tabela de frequência para cada uma das variáveis.
- Sexo
Contabilizado temos:
- Frequência Relativa Frequência Percentual
- Frequência Relativa Frequência Percentual
Feminino:
Masculino:
Passo 2
- Raça
A:
B:
P:
N:
Passo 2
b)
Resposta
a)
b)
Exercício Resolvido #2
Elaboração própria
Os dados abaixo representam o índice de alcalinidade de certa experiência.
- Construa a distribuição de frequência para dados grupados (utilizando a Regra da Raiz)
- Construa Histograma e Polígono de frequência.
Passo 1
Como queremos dados grupados, temos que dividir os valores em classes.
O exercício pede pra usarmos a regra da raiz.
Se a gente tem 45 valores:
Vamos ter então 7 classes.
Passo 2
O maior valor que temos é 95,2 e o menor é 25,2.
A amplitude total da amostra é então:
Com isso, cada classe vai ter uma amplitude igual a:
Ou seja vamos ter classes de 10 em 10:
Passo 3
(a)
pra construir a distribuição de frequência vamos montar uma tabela com:
Que é quantos valores existem dentro de cada classe;
Só ir somando as anteriores;
Que é dividir pelo total de valores que no caso são 45;
Que é dividir pelo total de valores (45).
Passo 4
Ficaria algo assim:
Passo 5
(b)
Construindo o nosso histograma e o polígono de frequência:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
UERJ - Lista 1- Prof Fabiano
Os dados abaixo representam o índice de alcalinidade de certa experiência.
- Construa a distribuição de frequência para dados grupados (utilizando a Regra da Raiz)
- Encontre as Medidas de Posição.
- Encontre as Medidas de Dispersão.
- Construa Histograma e Polígono de frequência e analise a curva.
- Analise os resultados.
Passo 1
Como queremos dados grupados, temos que dividir os valores em classes.
O exercício pede pra usarmos a regra da raiz.
Se a gente tem 45 valores:
Vamos ter então 7 classes.
Passo 2
O maior valor que temos é 95,2 e o menor é 25,2.
A amplitude total da amostra é então:
Com isso, cada classe vai ter uma amplitude igual a:
Ou seja vamos ter classes de 10 em 10:
Passo 3
(a)
pra construir a distribuição de frequência vamos montar uma tabela com:
Que é quantos valores existem dentro de cada classe;
Só ir somando as anteriores;
Que é dividir pelo total de valores que no caso são 45;
Que é dividir pelo total de valores (45).
Passo 4
Ficaria algo assim:
Passo 5
(b)
Medidas de posição são: média, moda e mediana.
Para dados grupados calculamos a média usando:
Passo 6
Para calcular a moda, temos primeiro que achar a classe modal que é a classe com a maior frequência absoluta.
No casso é a classe que tem .
Aí usamos a fórmula:
Passo 7
Pra calcular a mediana, temos primeiro que identificar a classe da mediana.
Para isso calculamos o valor de que será .
Agora, olhando para os valores de procuramos em qual classe estará o valor 22,5. Percebemos que a classe tem . Como queremos 22,5 não usaremos essa e sim a seguinte.
No nosso caso a classe da mediana será .
Ai usamos a fórmula:
Passo 8
(c)
Medidas de dispersão são: variância, desvio padrão e coeficiente de variação.
Para a variância vamos usar a fórmula:
Desvio padrão:
Coef. De variação:
Passo 9
(d)
Construindo o nosso histograma e o polígono de frequência:
A curva é assimétrica, pois
Passo 10
(e)
Temos que dizer se a curva é homogênea ou não.
Como o valor do é pequeno, a distribuição é dita homogênea.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
PUCRIO – Prova 1 - 2014.2
Os quadros abaixo correspondem aos resultados dos pesos dos alunos matriculados em uma das turmas na matéria de Probest 2013-2:
Com relação aos quadros apresentados acima, responda as perguntas:
- A quantidade de alunos com peso menor ou igual a .
- A quantidade de alunos com peso maiores de .
- Que tipo de simetria podemos verificar na amostra? Por quê?
- Com relação a Curtose, que tipo de curva podemos verificar na amostra? Por quê?
- Pelos dados da amostra, qual o coeficiente de variação?
- Pelos dados da amostra, qual o peso que mais se repete?
- Construa o diagrama de Pareto desta amostra, montando em blocos conforme o quadro do diagrama de frequência. Esboce os gráficos de frequência e cumulativo, mostrando os valores correspondentes.
Passo 1
(a)
É só ir somando as frequências até o intervalo que termina em .
Passo 2
(b)
Agora é só somar os que estão acima do intervalo que começa com , contando esse intervalo né.
Passo 3
(c)
Pra gente saber a assimetria, temos que comparar a média e a mediana, certo? Igual a gente viu lá na teoria. A gente tem então:
Esses valores eu tirei da tabela.
Como..
Temos assimetria positiva, que já tá na tabela lá, .
Passo 4
(d)
Vamos analisar o coeficiente de curtose que a gente tem.
Na tabela a gente vê que esse coeficiente é igual a . Como a gente sabe para coeficientes maiores que zero temos excesso de curtose, ou curtose leptocúrtica.
Passo 5
(e)
Coeficiente de variação tem uma fórmula, você lembra? Tranquilo, eu também não lembro... mas ai é só anotar aí, é o desvio padrão dividido pela média.
Esses dois valores a gente tem na nossa tabela, então é só dividir.
Passo 6
(f)
O peso que mais se repete é a moda, que também está na tabela.
Passo 7
A tabela que a gente tem é:
Pra fazer o diagrama de pareto primeiro vamos colocar esses valores em ordem decrescente de frequências, calcular suas frequências acumuladas (somando as anteriores) e o acumulativo que a gente precisa mostrar no gráfico.
Com isso, nosso diagrama de pareto seria assim... com o gráfico de barra representando as frequências e o gráfico das frequências acumuladas.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração Própria
Crie dois gráficos de barras, um com a frequência absoluta e outro com a frequência relativa, do número de alunos ausentes durante os cinco anos de curso na universidade.
Passo 1
Para o gráfico de frequência absoluta, organizamos os anos no eixo horizontal e as frequências no eixo vertical, e temos isso aqui:
Passo 2
Para as frequências relativas, primeiro somamos todas as ausências:
E aí calculamos as relativas:
Plotando esses valores no eixo vertical e mantendo os anos na horizontal temos:
Resposta
