Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Erro Absoluto de Estimação

Ver Todos os Exercícios

Teoria

O erro absoluto é a diferença entre o valor medido e o valor real, por exemplo, você mediu sua mesa e descobriu que ela tem , mas na realidade ela tem . Para calcular o erro absoluto, você usa a seguinte fórmula:

Onde é o valor medido e é o valor real. Substituindo, teremos:

📢 Clique para ver mais:

Mas afinal…se você esta medindo sua mesa é porque você não tem a medida real dela! Então como vamos calcular o erro absoluto?! 🤣🤣🤣 Pra isso a gente vai usar outras ferramentas da estatística! Bora conferir? 👇

Erro Absoluto de Estimação

O erro absoluto de estimação é a diferença entre a média amostral e a média populacional em módulo. A média populacional funciona como a “medida certa” que falamos ali em cima, no exemplo da nossa mesa ela poderia ser a medida que o fabricante diz que a mesa tem, por exemplo!

Como Calcular o Erro de Estimação

Vamos direto para ao que interessa, como fazemos os cálculos! Eu vou te mostrar a fórmula que vamos usar, mas não se assusta, ok?

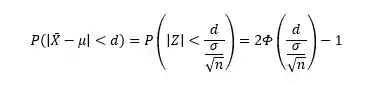
Erro de Estimação: Fórmula
Erro de Estimação: Fórmula

Agora bora entender o que essa fórmula esquisita significa! E pra começar com tudo, se liga nesse vídeo super completo sobre Erro de Estimação que o Responde Aí preparou pra você! 😉

separar

Erro Absoluto para Proporção

A gente também pode calcular o erro absoluto em problemas que envolvem proporção! Pra ficar mais claro vamos imaginar a seguinte situação:

Uma empresa fabrica pneus usados em carros importados. Digamos que tenha sido coletada uma amostra aleatória da linha de produção, com n=50 pneus, e que exatamente um número certo deles esteja fora das especificações. Vamos calcular a probabilidade de que o erro absoluto da estimativa da proporção fora das especificações não ultrapasse 0,05.

De acordo com o enunciado, d=0,05 e n=50, então o erro absoluto da estimativa da proporção é:

Para padronizar essa informação, vamos dividir tudo pelo desvio padrão. Lembrando que nesse caso e , então vamos ter que o desvio padrão é . Substituindo temos:

Substituindo os dados:

Agora é só seguir o mesmo processo de padronização que fizemos anteriormente. Dessa forma, ficaremos com:

Usando a tabela normal:

Isso quer dizer que em aproximadamente 52% dos casos o erro absoluto na estimação da verdadeira proporção de diodos fora das especificações não ultrapassaria 0,05!

Agora vamos praticar com exercícios?

Erro Absoluto de Estimação

Erro Absoluto para Proporção

Exercícios Resolvidos

Exercício Resolvido #1

João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 308.

Uma empresa fabrica diodos usados em placas de circuito impresso. Digamos que tenha sido coletada uma amostra aleatória da linha de produção, com n = 50 diodos, e que exatamente um número certo deles esteja fora das especificações. Deseja-se agora determinar a probabilidade de que o erro absoluto da estimativa da proporção fora das especificações não ultrapasse 0,05.

Passo 1

Primeiro vamos anotar os dados do problema.

Temos uma amostra com n = 50 .

E de acordo com o enunciado:

d = 0,05

O erro absoluto da estimativa da proporção é:

p ^ - p

A gente quer o que? A probabilidade desse erro não superar d .

P p ^ - p ≤ 0,05 =   ?

Passo 2

Pelo que a gente aprendeu, é só colocar na fórmula.

P p ^ - p ≤ 0,05 = 2 Φ 2 d n - 1

Aí a gente substitui os valores:

= 2 Φ 2 × 0,05 × 50 - 1

= 2 Φ 0,71 - 1                                          

Usando a tabela da Normal:

= 2 × 0,7611 - 1                                    

= 0,5222                                                                    

Isso quer dizer que em aproximadamente 52% dos casos o erro absoluto na estimação da verdadeira proporção de diodos fora das especificações não ultrapassaria 0,05.

Resposta

0,5222

Exercício Resolvido #2

João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 307.

Foi realizada uma pesquisa de opinião em uma grande empresa visando, entre outras coisas, determinar o nível médio de satisfação dos empregados com as condições de trabalho a eles oferecidas (instalações, equipamentos, etc).

O índice de satisfação de cada empregado pode ser medido em uma escala de zero a cem pontos, e sua variabilidade é tal que o desvio padrão populacional é da ordem de 30 pontos. Se nessa pesquisa foram sorteados 324 empregados ao acaso para uma entrevista, qual a probabilidade de que o índice de satisfação médio seja estimado com erro absoluto menor que três pontos?

Passo 1

Como sempre, primeiro vamos anotar os dados.

Temos uma amostra com n = 324 empregados.

E temos também o desvio padrão populacional σ = 30 .

O erro absoluto da estimação da satisfação média será:

x ¯ - μ

Temos que calcular a probabilidade desse erro ser menor que 3 pontos, ou seja, d = 3 .

P x ¯ - μ < 3 =   ?

Passo 2

Pra fazer isso é só a gente jogar na fórmula que a gente viu no conteúdo.

P x ¯ - μ < 3 = 2 Φ d σ n - 1

Substituindo os valores:

= 2 Φ 3 30 324 - 1

= 2 Φ 1,8 - 1                    

Usando a tabela da Normal.

= 2 × 0.9641 - 1  

= 0,9282                                  

Resposta

0,9282

Exercício Resolvido #3

P2- 2013.1 – UFRJ Estimador e Erros

Definimos a variável E = X -   μ como sendo o erro amostral da média, onde X é a média de uma amostra aleatória de tamanho n de uma população com distribuição Normal de média μ e desvio padrão σ = 20 .

  1. Que proporção das amostras de tamanho 100 terá o valor absoluto do erro amostral maior do que 2 unidades?
  2. Neste caso, qual deve ser o valor de δ para que P E > δ = 0,01 ?

Passo 1

(a)

O valor absoluto do erro é | E | , beleza?

O exercício quer a probabilidade..

P E > 2 =   ?

P X - μ > 2 =   ?

Padronizando...

P Z > 2 σ n =   ?

Onde σ = 20 e n = 100 ...

P Z > 1 =   ?

Usando os conhecimentos que a gente já tem lá da parte da Normal...

P Z > 1 = 1 - P Z < 1

= 1 - 2 Φ 1 - 1

= 2 - 2 Φ 1

Vendo o valor na tabela da Normal..

= 0,3174

Passo 2

(b)

Usando o mesmo raciocínio do item anterior, a gente chega na seguinte relação:

2 - 2 × Φ δ σ n = 0,01

Com isso...

Φ δ σ n = 2 - 0,01 2

Φ δ σ n = 0,995

Vendo na tabela a gente vê que:

δ σ n = 2,58

δ = 20 10 × 2,58 = 5,16

Resposta

a   0,3174

b   δ = 5,16

Exercício Resolvido #4

Elaboração Própria

Suponha que temos uma amostra de 40 estudantes e queremos estimar quantos dentre eles estão no último semestre da faculdade. Qual a probabilidade de que o erro absoluto da nossa estimativa seja menor que 0,02 ?

Passo 1

Aqui estamos lidando com um número de estudantes dentro de um número total, certo? Então o que queremos estimar é a proporção p de estudantes que estão para se formar. O nosso erro de estimação vai ser então:

| p ^ - p |

Queremos a probabilidade desse erro ser menor que 0,02 , então:

P p ^ - p < 0,02

Passo 2

Aplicando a fórmula vista na teoria:

P p ^ - p < 0,02 = 2 Φ 2 d n - 1

Onde d é a margem de erro, que é o máximo tolerável pedido, ou seja 0,02 , e n é o tamanho da amostra, no nosso caso, é 40 ). Então:

P p ^ - p < 0,02 = 2 Φ 2 × 0,02 40 - 1 = 2 Φ 0,25 - 1

Procurando z = 0,25 na tabela da normal, vemos que Φ 0,25 = 0 , 5987 , então:

P p ^ - p < 0,02 = 2 × 0,5987 - 1 = 0,1974

Resposta

19,74 %

Exercício Resolvido #5

Elaboração Própria

De uma população normal com σ   =   3 , retira-se uma amostra aleatória simples de tamanho 10 0 . Se quisermos garantir que uma análise do valor da média de alguma característica dessa população tenha o erro absoluto de estimação menor uma certa margem de erro com 90 % de confiança, qual deve ser a margem de erro adotada?

Passo 1

Nosso erro de estimação é em relação à média e vai é dado por:

| x - - x |

Nós queremos que esse erro seja menor que uma certa margem de erro d a um nível de confiança de 90 % . Dizer isso é a mesma coisa que escrever isso aqui:

P | x - - x | < d = 0,90

Queremos saber a probabilidade do erro ser menor que essa margem de erro!

Passo 2

Para descobrir esse d , podemos padronizar essa probabilidade, dividindo os dois lados da inequação ali dentro por σ n :

P | x - - x | σ n < d σ n = P Z < d σ n

Usando as propriedades do módulo na Normal temos:

P Z < d σ n = 2 Φ d σ n - 1

Mas nós sabemos que essa probabilidade tem que valor 0,90 , então:

2 Φ d σ n - 1 = 0,90

Φ d σ n = 0 , 95

Procurando 0,95 no corpo da tabela da Normal achamos o z = 1,64 , então:

d σ n = 1,64

Substituindo σ = 3 e n = 100 como dado no enunciado:

d 3 100 = 1,64 → d = 0,492

Resposta

49,2 %

Exercícios de Livros Relacionados

Definimos a variável e =X – μ como sendo o erro amostral de média. Suponha que a variância dos salários de uma certa região seja 400 reais². Qual deve ser o tamanho da amostra para que 95% dos erros a
Os dados da Tab. 14.7 foram obtidos para a distribuição da espessura do lenho em postes telefônicos. (W. A. Shewhart, Economic Control of Quality of Manufactured Productz, Macmillan and Co., New York,
Uma variável aleatória X tem fdp f x = β + 1 x β , 0x1 . Calcule a estimativa de MV de β , baseada numa amostra X1, ..., Xn. Calcule a estimativa quando os valores amostrais forem: (0,3;0,8;0,27;0,35;
Um procedimento é realizado até que um particular evento A ocorra pela primeira vez. Em cada repetição, P A = p ; suponha que sejam necessárias n1 repetições. Depois, esse experimento é repetido e, ag
Suponha que 200 observações independentes X 1 , … ,X 200 sejam obtidas de uma variável aleatória X. Sabe-se que ∑ X i = 300 e que ∑ X i ² = 3 754 ² . Empregando esses valores, Calcule uma estimativa n