Dimensionamento da Amostra com Desvio Padrão
Produzido por Jorge Alberto NascimentoTeoria
Qual deve ser o tamanho mínimo de uma amostra?
Esse é um questionamento muito comum sempre que alguém vai coletar dados pra fazer uma estimativa. Teoricamente, quanto maior a amostra, melhor a estimativa, mas também maior é o custo da pesquisa.
Pra solucionar esse dilema, a gente pode estabelecer um tamanho mínimo pra amostra de acordo com o nível de precisão que a gente quer.
Pra fazer isso, vamos primeiro definir duas variáveis:
- distância máxima tolerável entre a estimativa e o valor correto do parâmetro.
- probabilidade de que essa distância seja maior do que .
Isso quer dizer que:
Concorda? Beleza.
A gente vai ter 3 diferentes jeitos de realizar essa conta dependendo dos dados que a gente tem. A gente pode dimensionar amostras:
- Pra estimar o valor da média populacional , sabendo o valor do desvio padrão populacional, .
- Não conhecendo o valor de .
- Pra estimar o valor da proporção populacional.
Vamos entender melhor caso a caso.
COM D.PADRÃO CONHECIDO
Pra estimar o valor da média populacional , sabendo o valor do desvio padrão populacional, , a gente vai trabalhar com a fórmula de cima ali né.
Primeiro, falar
É o mesmo que:
Só usamos a propriedade de complementar aqui, beleza?
Cara, lembra que ?
Do lado esquerdo a gente tem , certo? Ta sentindo um cheirinho de padronização aqui? Pois,
Certo?! Ou seja, vamos dividir dos dois lados por , ficando com:
Que é a mesma coisa que:
Usando aqueles paranauês da normal, ficamos com:
Esse valor de a gente pega na tabela, lembra? A gente calcula o valor de e procura o valor de que gera essa probabilidade. É só procurar pelo valor de no interior da tabela da Normal e ver qual o valor de referente, juntando o valor da primeira coluna com o da primeira linha. É isso que eu quero dizer com .
Não entendeu? Pera, eu desenho! Isso você não pode errar.
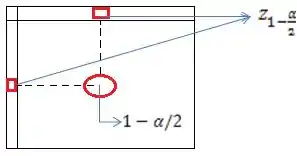
Tá safo agora?
Com isso a gente chega em:
Pronto! Esse é justamente o tamanho da nossa amostra. Percebe que você tem que conhecer o valor de nesse caso?
Exemplo: Qual deveria ser o tamanho da amostra de empregados a serem entrevistados para que o erro absoluto na estimação do índice de satisfação média estivesse limitado em 1,5 unidades com probabilidade de ? Sabendo que o desvio padrão populacional é 30 unidades.
Passo1) Calcular o .
Pelo enunciado:
Passo2) Calcular .
Pra isso eu usei a tabela, se você procurar no interior dela o valor 0,9641 vai ver que o valor de referente é 1,8.
Passo3) Calcular .
COM D.PADRÃO DESCONHECIDO
Bom, mas se eu não tenho o valor da média populacional, é de se esperar que eu também não conheça o valor do desvio padrão populacional, concorda?
O que fazer nesse caso então?
Bem tranquilo, quando isso acontecer, em vez da gente usar o valor de , a gente usa o valor do desvio padrão amostral, .
Ficaria assim:
O resto continua a mesma coisa. A única diferença mesmo é que a gente vai ter que calcular .
Esqueceu como faz isso? Relaxa, se o enunciado não te der isso pronto, basta calcular a variância amostral e tirar a raiz quadrada.
A fórmula da variância amostral é a seguinte:
Onde é a média amostral.
Exemplo: Qual deveria ser o tamanho da amostra de empregados a serem entrevistados para que o erro absoluto na estimação do índice de satisfação média estivesse limitado em 1,5 unidades com probabilidade de ? Sabendo que o desvio padrão amostral é 30 unidades.
Passo1) Calcular o .
Sabemos que
Pelo enunciado:
Passo2) Calcular .
Pois sabemos que
Queremos saber qual Z resultar nessa probabilidade. Nessa parte temos que voltar na tabela lembra?
Se você procurar no interior dela o valor 0,9641 vai ver que o valor de referente é 1,8.
Passo3) Calcular .
COM D.PADRÃO CONHECIDO
COM D.PADRÃO DESCONHECIDO
Exercícios Resolvidos
Exercício Resolvido #1
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 309.
Foi realizada uma pesquisa de opinião em uma grande empresa visando, entre outras coisas, determinar o nível médio de satisfação dos empregados com as condições de trabalho a eles oferecidas (instalações, equipamentos, etc).
O índice de satisfação de cada empregado pode ser medido em uma escala de zero a cem pontos, e sua variabilidade é tal que o desvio padrão populacional é da ordem de 30 pontos. Qual deveria ser o tamanho da amostra de empregados a serem entrevistados para que o erro absoluto na estimação do índice de satisfação médio estivesse limitado em 1,5 unidades com a probabilidade de 92,81% ?
Passo 1
Nesse caso a gente quer dimensionar uma amostra e já conhecemos o desvio padrão..
A fórmula que vamos utilizar é:
De acordo com o enunciado sabemos também que:
Passo 2
Calcular e .
Passo 3
Agora é só jogar na fórmula..
Resposta
Exercício Resolvido #2
P2- 2013.1 – UFRJ Dimensionamento de amostras
Definimos a variável como sendo o erro amostral da média, onde é a média de uma amostra aleatória de tamanho de uma população com distribuição Normal de média e desvio padrão .
(c) Qual deve ser o tamanho da amostra para que o módulo do erro amostral seja inferior a 1 unidade com 95% de probabilidade?
Passo 1
(c)
Questão de dimensionamento de amostra com conhecido. Pela fórmula a gente tem que:
Agora é só fazer conta...
Substituindo os valores...
Resposta
Exercício Resolvido #3
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 332.
Usando os seguintes dados,
E admitindo que a média populacional é desconhecida, dimensione uma nova amostra dessa população que nos permita estimar de forma que o erro absoluto de estimação seja menor que 0,5 com probabilidade .
- Se o desvio padrão populacional é conhecido e igual a 2;
Passo 1
(a)
O estimador da média populacional é a média amostral .
O erro absoluto da estimação tem que ser menor que 0,5 com probabilidade de 98%.
Onde e
Calcular e .
Passo 2
Nesse primeiro caso temos , então estamos num caso de dimensionamento com conhecido.
Para calcular o valor de então, temos a fórmula:
Basta substituir os valores:
Como é número inteiro.