Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 4

11-4. Um artigo em Technomctrics. de S. C. Narula e J. F. Wellington Predhction, Lancar Regressien, anda Minimmon Ston of Relatire Errors"Previsão. Regressao Linear e Soma Minima dos Erros Relativos. Vol. apresenta dados de preços de vendas e taxas anuais para 24 casas.Esses dados são mostrados na seguinte tabela.

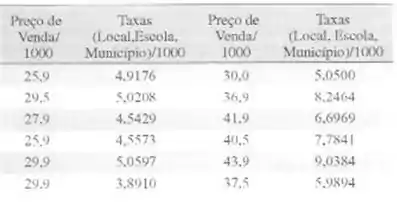
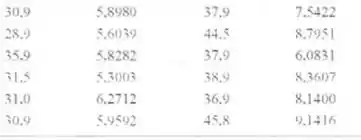
a) Considerando que um modelo de regressao linear simples seja apropriado. obtenha um ajuste por minimos quadrados. relacionando o

preço de venda as taxas pagas.

b) Encontre opreco médio de venda. dado que as taxas pagas são x - 7.50.

c) Calcule o valor ajustado de y correspondendo a.x = 5.8980. Encontre o residuo correspondente.

d)Calcule o valor ajustado ý, para cada valor de x, usado para ajustar o modelo. Construa então um gráfico de y, contra o valor observado corresponlente. y. e comente o que esse gráfico aparentaria se a relacão entre ye x fosse uma linha reta deterministiea (sem erro aleatorio). O) gráticoobtido indica realmente que as taxas pagas fepresen

tam uma variável efetiva de regressáo na previsáo do preco de venda!

Passo 1

Oi oi gente,

Vamos lá fazer mais uma questão passo a passo?

Vem comigo!

Dados:

Letra a:

As estimativas de mínimos quadrados da interceptação e inclinação são:

A linha de regressão de mínimos quadrados torna-se então:

Determine a soma dos erros quadrados:

é então estimado pela soma dos erros quadráticos divididos pelo tamanho da amostra diminuída por 2:

Passo 2

Letra b:

Substitua x na linha de regressão de mínimos quadrados por 7.5 e avalie:

Passo 3

Letra c:

Substitua x na linha de regressão de mínimos quadrados por 5.8980 e avalie:

O resíduo é o valor real diminuído pelo valor previsto:

Passo 4

Letra d:

O preço de venda/1000 está no eixo horizontal e os valores y ajustados estão no eixo vertical.

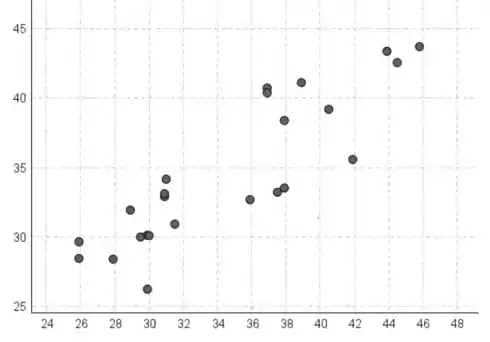
Não há curvatura forte presente no gráfico de dispersão, o que indica isso. os impostos pagos são uma variável regressora eficaz na previsão dos preços de venda.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No Problema6 , qual o tempo médio esperado para empacotar um volume com 30d m 3 ?

Com o modelo z ^ = α ^ + β ^ x para a acuidade visual, desenvolvido nos problemas anteriores:c) construa o I C com 95 % de confiança para a acuidade visual média dos indivíduos com80 anos. Comente o r

Os dados abaixo se referem a meses de experiência de dez digitadores e o número de erros cometidos na digitação de determinado texto.Dados: ∑ x i = 60 ,∑ x i 2 = 460 ,∑ y i = 170 ,∑ x i y i = 768 . b)

Os dados abaixo correspondem às variáveis renda familiar e gasto com alimentação numa amostra de dez famílias, representadas em salários mínimos. Obtenha a equação de regressãoy ^ = α ^ + β ^ x .b) Qu

Com o modelo z ^ = α ^ + β ^ x para a acuidade visual, desenvolvido nos problemas anteriores:b) construa o I C de 95 % para a acuidade visual esperada para indivíduos com30 anos de idade;