10-77. Uma miquina de teste de dureza Rockwell pressiona uma pon-
teira em um corpo-de-prova, usando a profundidade da depressão re-
sultante pura indicar a dureza. Duas ponteiras diferentes estao sendo
comparadas para determinar se clas fornecem as mesmas leituras de
dureza Rockwell na escala C. Nove corpos-de-prova sào testados.com
ambas as pomteiras sendo testadas em cada corpo-de-prova. Os dados
sao mostrados na tabela seguinte.
a) Estabeleca quaisquer suposicoes necessárias para testar a afirmacao
de que ambas a ponteiras produzem as mesmas leiturns de dureza Roxk
well na eseala C. Ventique essas suposicie's nos dados que vocé tem.
b) Aplique um método estatistico apropriado para kterminar se os
dados contirmam a afirmacão de quc a diferenca nas leituras de
dureza Rockwell na eseala C das duas ponteiras é signifieativamen-
te diterente de zero.
c) Supxmha que se as duas ponteiras diferin'm nas leituras da dureza media
por 1.0, vamos querer que a potencia do teste seja no minimo0.9. Paru
quantos corpos-de-prova devem ser usados no leste?
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dado:
Determine a diferença no valor para cada par de dados:
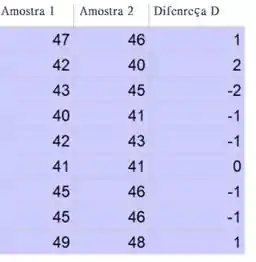
A média é a soma de todos os valores dividida pelo número de valores:
A variância é a soma dos desvios quadrados da média dividido por . O desvio padrão é a raiz quadrada da variância:
Passo 2
Letra a:
Exigimos que as distribuições sejam distribuídas aproximadamente normalmente.
Gráfico da probabilidade normal:
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com .
A menor pontuação padronizada corresponde à menor quantidade de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
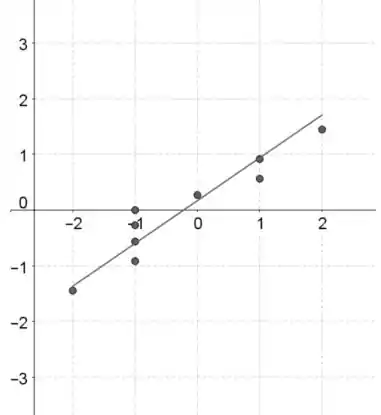
A suposição normal parece satisfeita, porque o padrão em ambos os gráficos de probabilidade normal é aproximadamente linear, o que indica que as distribuições são distribuídas aproximadamente normalmente.
Passo 3
Letra b:
Determine as hipóteses:
Determine a estatística de teste:
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t no na linha
Se o valor P for menor ou igual ao nível de significância, a hipótese nula é rejeitada:
Existem evidências científicas para apoiar a afirmação de que as duas pontas diferem significativamente de zero.
Passo 4
Letra c:
Dados:
é o complemento da potência:
Fórmula do tamanho da amostra:
é a hipótese nula em
é a hipótese alternativa
Determine usando a tabela lll (procure 0.005 na tabela. O valor z é então o valor z encontrado com sinal oposto):
Determine usando a tabela lll (procure 0.1 na tabela. O valor z é então o valor z encontrado com sinal oposto):
Preencha os valores conhecidos na fórmula e avalie (arredonda para cima!):
Resposta
- Suposição satisfeita
- Há evidências suficientes para apoiar a alegação de que as duas dicas são diferentes.