Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 5
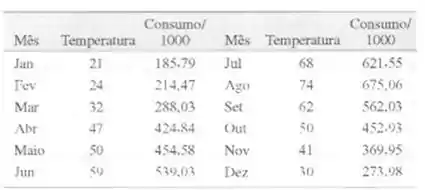
11-5. A quantidade de hbras de vapor usadas por més por uma planta
química está relacionada à temperatura ("Fj média amhiente para aque-
le mes. O consumo do ano passado e a temperatura são mostrados na
seguinte tabela:
a) Considerando que um modelo de regressäo lincar simples scja apro-
priado, ajuste o modelo de regressão relacionando o consumo de
vapor (v) com a temperatura média (x). Qual é a estimativa para o2?
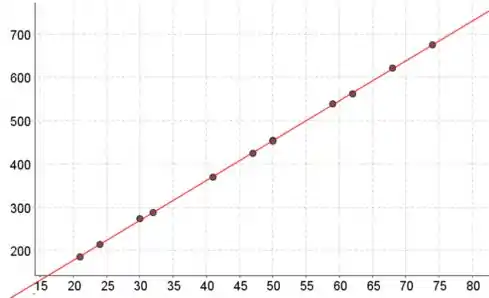
Faça um gráfico da linha de regressão.
b) Qual será a estimativa do consumo esperado de vapor quando a tem
peratura média for 55°F?
c) Que mudança no uso médio de vapor será esperada quando a tem-
peratura média mensal variar de 1°F?
d) Suponha que a temperatura média mensal seja de 47°F. Calcule o
valor ajustado de ye o resíduo correspondente.
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
Letra a:
As estimativas de mínimos quadrados da interceptação e inclinação são:
A linha de regressão de mínimos quadrados torna-se então:
Determine a soma dos erros quadrados:
é então estimado pela soma dos erros quadráticos divididos pelo tamanho da amostra diminuída por 2:
Passo 2
Letra b:
Substitua x na linha de regressão de mínimos quadrados por 55 e avalie:
Passo 3
Letra c:
Um aumento de 9.2084, porque a inclinação é 9.2084 e a inclinação é o aumento / diminuição média de y por unidade de x.
Passo 4
Letra d:
Substitua x na linha de regressão de mínimos quadrados por 47 e avalie:
O resíduo é o valor real diminuído pelo valor previsto:
Resposta
- Um aumento de