11-79. Um artigo na revista IEEE Transactions on Insirumeniation and
Measuremenm i"Direct. Fast, and Accurate Measurement of V, and K
of MOS Transistor Lising V,-Siti C'ircuit"'' Medida Direta. Rápida c
Exata de V, e Kde um Transistor MOS. usando um Circuito V, Sifi".
Vol. 40, 1991. p. 951 955) desereveu o uso de um modelo de regres
são linear simples para expressar a corrente (cm mA). v. como uma
função da diferença de voltagem (em V). O)s dados são apresentados
a seguir:

a) Desenhe um diagrama de dispersão desses dados. Uma relação lincar
parece plausível?
b) Ajuste um modelo de regressão lincar simples a esses dados.
c)Teste a signiticância da regressão usando a - 0,05. Qual é o valor
P para csse teste?
d) lincontre um intervalo de confiança de 95% para a inclinação esti-
mada.
e) Teste a hipótese .-0 contra H,: 4 O usando a =0.05. Quc
conclusoes você pode tirar?
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
Letra a:
Denote a variável de tensão terra-fonte com a letra x, e a variável aleatória da corrente de dreno com a letra y. Então, após o processamento, os dados aparecem na tabela. Chegamos ao seguinte gráfico de dispersão dos dados:
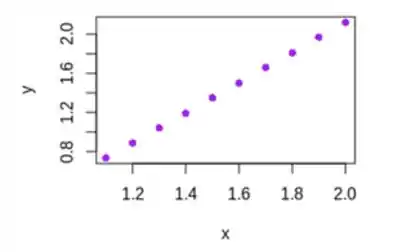
Vemos que a relação em linha reta é muito bem esperada neste problema. Prosseguimos, para ajustar o modelo linear:
Passo 2
Letra b:
Primeiro, vamos calcular as quantidades importantes (observe :
Agora estamos prontos para determinar os coeficientes do modelo:
Portanto, o melhor ajuste linear para os dados é:
Passo 3
Letra c:
Precisamos testar a significância da regressão. Neste exercício, vamos optar pela abordagem de análise de variância para este problema. Primeiro, vamos avaliar a regressão e a soma dos quadrados dos erros:
Para calcular o valor da estatística F:
Rejeitamos Ho se , então primeiro determine:
e então, rejeitamos por causa da enorme estatística de teste que obtivemos.
Portanto, o modelo é significativo.
Passo 4
Letra d:
O intervalo de confiança da inclinação é dado pela seguinte fórmula:
Portanto, calculamos:
e obtemos:
Passo 5
Letra e:
Primeiro obtenha o erro padrão do coeficiente:
e então calculamos a estatística de teste:
para concluir, rejeitamos a hipótese nula de em favor da alternativa bilateral porque:
E, então,
Resposta
- Sim