Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 80
11-80. A resistencia do papel usado na fahricação de caixas de pape-
lāo, v. está relacionada a porcentagem da concentração de madeira de
lei na polpa original, r. Sob condições controladas. uma planta piloto
fabrica Ih amostras.cada uma sendo proveniente de uma balelada di-
ferente de polpa. Mede-se a resistência à tração. Os dados sào mostrados aqui
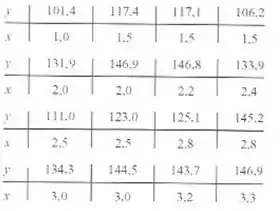
a) Ajuste um moxlelo de regressão linear simples aos dados.
b) Teste a significância da regressão usando = 0.05.
c)Construa um intervalo de confiança de 90% para a inclinação .
d)Construa um intervalo de contiança de 9052 para a interseção Bu.
e) Construa um intervalo de confianca de 9556 para a resiténcia mé-
dia em .x = 2.5.
f) Analise os residuos e comente a adequação de modelo.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
Denotemos a variável da porcentagem de concentração de madeira de lei com a letra x, e a variável aleatória de resistência à tração com a letra y.
Letra a:
Primeiro, vamos calcular as quantidades importantes (nota :
Agora estamos prontos para determinar os coeficientes do modelo:
Portanto, o melhor ajuste linear para os dados é:
Passo 2
Letra b:
Precisamos testar a significância da regressão. Neste exercício, vamos optar pela abordagem de análise de variância para este problema.
Primeiro, vamos avaliar a regressão e a soma dos quadrados dos erros:
Para calcular o valor da estatística F:
Rejeitamos então primeiro determine:
E, em seguida, vamos rejeitar .
Portanto, o modelo é significativo.
Passo 3
Letra c:
O intervalo de confiança da inclinação é dado pela seguinte fórmula:
Portanto, calculamos, com o dado nesta parte do exercício:
E obtemos:
Passo 4
Letra d:
Da mesma forma que na parte anterior, o intervalo de confiança da interceptação é dado pela seguinte fórmula:
Portanto, calculamos, com o dado nesta parte do exercício:
E obtemos:
Passo 5
Letra e:
Vamos lembrar que: o significado do modelo de regressão é a seguinte relação:
Podemos estimar os parâmetros para obter a estimativa pontual desta expectativa condicional (resposta média):
Agora lembre-se da fórmula para o intervalo de confiança de na resposta média em:
Agora calcule as quantidades necessárias a partir dos dados (ou use já calculado) para encontrar:
Passo 6
Letra f:
Trace os resíduos do modelo contra os valores ajustados para a resposta e examine. Notamos que os resíduos tendem a ser menores na cauda do que no meio. Além disso, o modelo de fato parece ser adequado, mas isso não pode ser ignorado.
Resposta
- Ver resolução