11-84. Um artigo em Air and Waste ("lipdate on Ozonc Trends in

Caltfornia's Seuth Coust Air Busin" - Atualidades sobre as Tendên-

cias de Ozônio em Bacias Acreas da Costa Sul da Califórnia. Vol. 43.

1993) estudou os níveis de ozônio em bacias acreas da costa sul da

Calhtormia. durante o periodo de 1976 1991. O) autor acredita que o

nimero de dias que o nivel de ozonio excede 0.20 partes por milhão

dependa do indice sazonal meteorológico (a temperatura média sazo-

nal a 850 milibar). Os dados são:

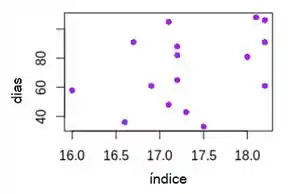
a) Construa um diagrama de dispersão dos dados.

b) Ajuste um modelo de regressão linear simples a esses dados.Teste

a signilicancia da regressāo.

c) Encontre um IC de 95% para a inclinação

d)Analise os residuos e comente a adequação do modelo.

Letra b:

Primeiro, vamos calcular as quantidades importantes (nota ):

Agora estamos prontos para determinar os coeficientes do modelo:

Portanto, o melhor ajuste linear para os dados é:

Precisamos ainda testar a significância da regressão. Neste exercício, vamos optar pela abordagem de análise de variância para este problema.

Primeiro, vamos avaliar a regressão e a soma dos quadrados dos erros:

Rejeitamos , então primeiro determine:

e concluímos que não rejeitamos porque .

O modelo é, portanto, insignificante com . (Embora fosse significativo com )

Letra c:

O intervalo de confiança da inclinação é dado pela seguinte fórmula:

Portanto, calculamos: (:

e obtemos:

Letra d:

Vamos traçar, os resíduos contra os valores ajustados e examine o gráfico:

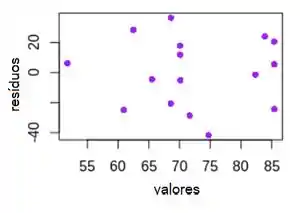
Concluímos que o modelo não é adequado. Nem é significativo, nem nenhum dos resíduos parece absolutamente ótimo (embora promissor)