Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 6.Exercícios - Ex. 94
Em 1789, Henry Cavendish estimou a densidade da Terra usando uma balança de torção. Suas 29 medidas estão apresentadas a seguir, expressas como múltiplos a densidade da água.
- Calcule a média desvio padrão e a mediana da mostra dos dados Cavendish para densidade.
- Construa um gráfico de probabilidade normal dos dados. Comente o gráfico. Parece haver um Outlier “baixo” nos dados?
- A mediana da amostra meira melhor estimativa da densidade da terra do que a médica da amostra? por quê?
Passo 1
Letra a:
O número total da amostra dos dados de Cavendish é 29.
A média dos dados de Cavendish é 5.4197.
O desvio padrão dos dados de Cavendish é 0.3389.
A mediana dos dados de Cavendish é 5.4600.
Passo 2
Letra b:
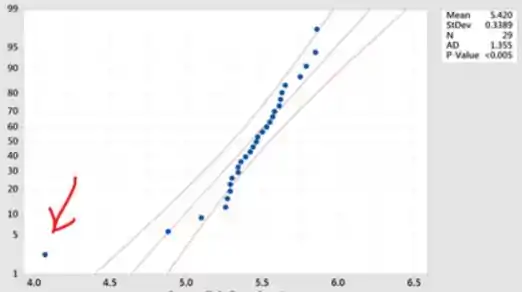
O gráfico de probabilidade da densidade de Cavendish_1 (normal-95% CI):
O eixo x é a densidade de Cavendish e o eixo y é a porcentagem:
Passo 3
Letra c:
Sim, parece haver um outlier "baixo" nos dados. Este ponto corresponde ao valor de densidade em 4.07 e porcentagem de 2.38095.
Além disso, com o gráfico de probabilidade normal podemos concluir que os dados não são normalmente distribuídos.
Resposta
- O número total da amostra dos dados de Cavendish é 29.
- Ver gráfico
- Sim, parece haver um outlier "baixo" nos dados. Este ponto corresponde ao valor de densidade em 4.07 e porcentagem de 2.38095.
A média dos dados de Cavendish é 5.4197.
O desvio padrão dos dados de Cavendish é 0.3389.
A mediana dos dados de Cavendish é 5.4600.
Além disso, com o gráfico de probabilidade normal podemos concluir que os dados não são normalmente distribuídos.