Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 89

Suponha que X e Y tenham uma distribuição normal bivariada com σ x = 4 ,   σ y = 1 ,   μ x = 4 ,   μ y = 4 e ρ =   - 0.2 . Desenhe uma curva de nível aproximada da função densidade de probabilidade conjunta.

Passo 1

Sejam X e Y com uma distribuição normal bivariada com parâmetros

σ x = 4 ,   σ y = 1 ,   μ x = 4 ,   μ y = 4 e ρ =   - 0.2

A função de densidade de probabilidade conjunta necessária é:

f X Y ( x , y ) = 1 2 π σ X σ Y 1 - p 2 × e { - 1 2 ( 1 - p 2 ) ( x - μ X σ 2 X - 2 ρ ( x - μ X ) ( y - μ Y ) σ X σ Y + ( y - μ Y ) 2 σ 2 Y }

= 0.40610 e x p { - 0.03255 ( x - 4 ) 2 - 0.05208 ( x - 4 ) ( y - 4 ) - 0.52083 ( y - 4 ) 2 }

Passo 2

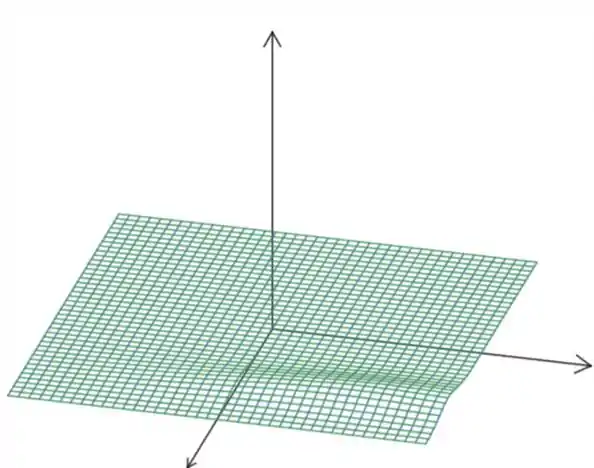
E o gráfico é:

Resposta

0.40610 e x p { - 0.03255 ( x - 4 ) 2 - 0.05208 ( x - 4 ) ( y - 4 ) - 0.52083 ( y - 4 ) 2 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Lançam-se dois dados perfeitos. X indica o número obtido no primeiro dado e Y o maiorou o número comum nos dois dados. Escreva por meio de uma tabela de dupla entrada a distribuição conjunta de X e Y.
Uma moeda perfeita é lançada três vezes. Sejam:X: número de caras nos dois primeiros lançamentos;Y: número de caras no terceiro lançamento; eS: número total de caras.Calcule a média e a variância das
Lançam-se dois dados perfeitos. X indica o número obtido no primeiro dado e Y o maiorou o número comum nos dois dados. Calcule as esperanças e variâncias de X e Y.
Lançam-se dois dados perfeitos. X indica o número obtido no primeiro dado e Y o maiorou o número comum nos dois dados. Calcule Var(X + Y).
O exemplo a seguir ilustra que ρ = 0 não implica independência. Suponha que (X, Y)tenha distribuição conjunta dada pela tabela abaixo. Justifique por que X e Y não são independentes.