Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 114
9-114. Considere os dados de qualidade de água do Exercicio 6-24.
(a) Esses dados suportam a afirmação de que a concentraçio média de
sólidos suspensos não excede 50 partes por milhão? Use a - 0,05.
(b) Qual e o valor P para o teste do item ta?
(c) A distribuição normal parece ser um modelo razoável para esses
dados? Faça um teste apropriado de adequação de ajuste para res-
ponder essa questão.
Passo 1
E aiii gente, tudo bom??
Vamos começar a resolvar essa questão que é super tranquila!
Confia em mim
Dado:
Valores dados:
A média é a soma de todos os valores dividida pelo número de valores:
A variância é a soma dos desvios quadrados da média dividida por . O desvio padrão é a raiz quadrada da variância:
Passo 2
Letra a:
Determine as hipóteses:
Determine o valor da estatística de teste:
O valor P é a probabilidade de obter o valor da estatística de teste ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela V contendo o valor t na linha :
Se o valor P for menor ou igual ao nível de significância, a hipótese nula é rejeitada:
Há evidências suficientes para apoiar a alegação de que a concentração média de sólidos suspensos não excede 50 partes por milhão.
Passo 3
Letra b:
O valor P na parte (a) foi .
Passo 4
Letra c:
O valor z é a quantidade diminuída pela média dividido pelo desvio padrão dividido pela raiz quadrada do tamanho da amostra. Determine a probabilidade nos intervalos/classes (de sua escolha) usando a tabela III:
A hipótese nula afirma que as proporções da população são todas iguais:
A hipótese alternativa afirma o oposto da hipótese nula:
Determine as frequências observadas (frequências dos valores dentro da classe).
As frequências esperadas são o produto do tamanho da amostra n e as probabilidades .
Os subtotais do qui-quadrado são as diferenças de quadrados entre as frequências observadas e esperadas, divididas pela frequência esperada.
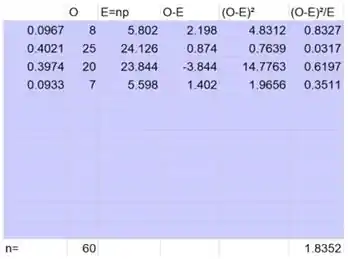
O valor da estatística de teste é então a soma dos subtotais qui-quadrado:
O valor P é a probabilidade de obter o valor da estatística de teste ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela IV contendo o valor na linha :
Se o valor P for menor ou igual ao nível de significância, a hipótese nula é rejeitada:
Não há evidências suficientes para rejeitar a alegação de uma distribuição normal.
Resposta
- Há evidências suficientes para apoiar a alegação de que a concentração média de sólidos suspensos não excede 50 partes por milhão.
- Não há evidências suficientes para rejeitar a alegação de uma distribuição normal.