Enunciado
Probabilidade e Estatística - Barbetta - Estatística Aplicada a Ciências Sociais- Ed: 1º - Capítulo 3.Exercícios - Ex. 2
Ainda com respeito ao Exemplo 3.4, suponha que o tempo de serviço destes funcionários, em anos completos, são os valores seguintes:
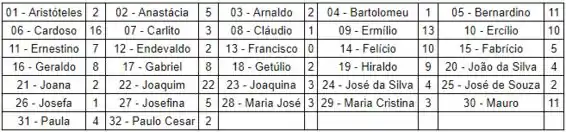
Apresente a amostra da variável tempo de serviço associada à amostra de funcionários obtida no Exercício 1.
Passo 1
Oiiie, tudo certinho? Vamos começar mais um dia de estudos?
Esse problema veio do livro do Barbetta nomeado “Estatística aplicada a ciências sociais” 5ª Edição. Essa informação é relevante pois são necessárias para a resolução do exercícios informações que estão no apêndice do livro assim como ao longo do Capítulo 3. Eu vou tentar resumir as informações aqui da melhor maneira possível.
No exemplo 3.4 temos um conjunto de 32 funcionários de uma empresa e que representa a nossa população, os nomes destes funcionários são os seguintes:
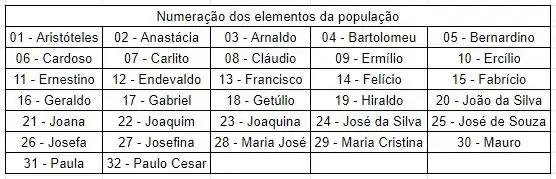
No exercício 1, tomamos uma amostra com 10 elementos através da Tabela I no apêndice do livro, nos dando a seguinte enumeração:
18, 32, 15, 09, 19, 30, 10, 04, 06 e 27.
Que então estabelecem nossa amostra como:
A = {Getúlio, Paulo Cesar, Fabrício, Ermílio, Hiraldo, Mauro, Ercílio, Bartolomeu, Cardoso, Josefina}
Muito bem, no próximo passo usemos essa amostra para construir a amostra desta nova variável.
Passo 2
Para identificarmos a amostra desta nova variável, apenas precisamos identificar quais são os tempos de serviço de cada elemento da amostra A individualmente, portanto, se temos a variável aleatória T, temos que ela está relacionada a seguinte amostra:
T = {2, 2, 5, 13, 9, 11, 10, 1, 16, 5}
E assim terminamos mais uma questão! Te vejo na próxima!!
Resposta
Ao longo do passo 2.