Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 6.Exercícios - Ex. 78
Uma amostra com seis resisto Oris resultou na seguinte resistências
.
- Calcule a variância o desvio padrão da amostra.
- Subtraia 35 de cada uma das medidas originais de resistência e calcule. Compare os resultados com aqueles obtidos no item à explique sua resposta.
- Se as resistências fossem
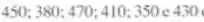ohms. Você poderia usar os resultados dos itens anteriores desse Problema para encontrar s^2 e s?
Passo 1
Os dados são os seguintes:
e
Letra a:
Vamos calcular a variância e o desvio padrão da amostra.
Para descobrir isso, primeiro temos que determinar a média da amostra.
A variância da amostra é:
O desvio padrão da amostra é:
Passo 2
Letra b:
Vamos subtrair 35 de cada uma das medidas de resistência originais e calcular e s
Então, temos:
A média da amostra:
A variância da amostra:
O desvio padrão da amostra:
À medida que cada valor diminui em 35, também diminui em 35, mas não é afetado, portanto, a variância e o desvio padrão da amostra permanecem o mesmo.
Passo 3
Letra c:
Se multiplicarmos cada um dos valores da amostra por 10, a média e todos os valores aumentariam 10 vezes.
Portanto, a variância aumentaria 100 vezes, e o desvio padrão da amostra 10 vezes.
Resposta
- e
- e
- Se multiplicarmos cada um dos valores da amostra por 10, a média e todos os valores aumentariam 10 vezes.
Portanto, a variância aumentaria 100 vezes, e o desvio padrão da amostra 10 vezes.