Analise os dados desse experimento.
Encontre um modelo apropriado de regressão que explique à vida
da ferramenta, em termos das variáveis usadas no experimento.
Analise os resíduos desse experimento.
Passo 1
Bom galera, para o experimento fatorial , temos a tabela:
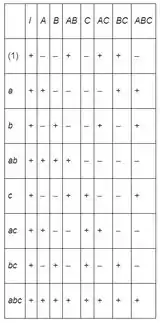
Encontrando as médias dos dados para cada fator. Os resultados estão resumidos na tabela abaixo. Observe que .
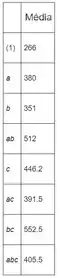
Passo 2
Belezinha, usando a tabela de sinais para calcular o efeito de . Adicionando os efeitos com os sinais correspondentes na coluna do fator considerado.
Todos os outros efeitos são encontrados da mesma forma. A tabela dos efeitos para todos os fatores e interação é dada por:
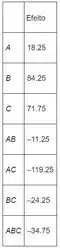
Examinando a magnitude dos efeitos mostra que os fatores e são dominantes. Se o for significativo, devemos concluir que a também é significativa.
Agora realizando a analise de variância:
Passo 3
Agora, calculando todas as outras somas de quadrados da mesma forma. O resultado está resumido na tabela:
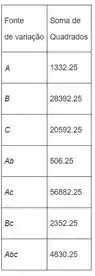
A soma total dos quadrados é:
E a soma dos quadrados para o erro:
Passo 4
Então, cada para um fator ou interação tem grau de liberdade, tem graus de liberdade, tem graus de liberdade. Encontrando cada como a razão de e correspondentes. O resultado é:

Encontramos o valor estatístico para cada fator e interação como uma razão correspondente para . O resultado fica:
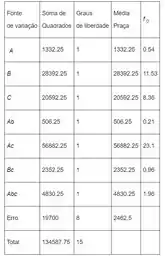
Passo 5
Agora, nós usamos o software para encontra os valores, e encontramos:
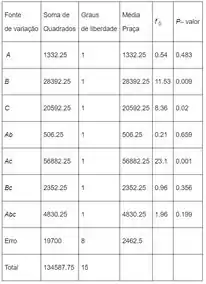
Procuramos fatores com pequenos valores, tais fatores são , e a interação . Esse resultado concorda com a análise dos efeitos dos fatores. Portanto, os fatores , , e a interação devem ser considerados significativos.
Passo 6
Construimos um modelo de regressão linear para os fatores , , e . A constante é estimada pela média geral, e os coeficientes de regressão são estimados pela metade das estimativas de efeito correspondente. O modelo de regressão é:
Passo 7
Usaremos Minitab para construir o gráfico de probabilidade normal e as parcelas de resíduos versus o valor montado e cada regressor. Use e como valores baixos e elevados para os dados correspondentes para se encaixar na linha de regressão em parte . O gráfico de probabilidade normal e os outros resíduos são:

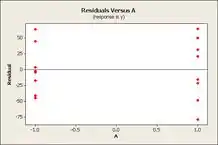

O enredo de probabilidade normal mostra que não há saídas da normalidade. As parcelas residuais versus o valor ajustado e os regressores mostram distribuição bastante simétrica dos pontos cerca de . Portanto, podemos concluir que o modelo de regressão encontrado em parte é adequado.
Resposta
Ei, a resposta está no passo a passo :)