Estabeleça as hipóteses de interesse nesse experimento.
Teste as hipóteses anteriores e tire conclusões, usando a análise de variância com .
Analise graficamente a interação.
Analise os residuos desse experimento.
Usando o método de Fisher, investigue as diferenças entre densidade média do ânodo nos três níveis diferentes de temperatura. Use .
Passo 1
Bom galera, podemos montar uma tabela com os fatores estudados e fica:
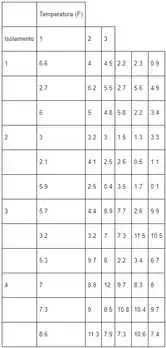
E o modelo é:
As hipóteses devem ser testadas da seguinte forma:
E:
Passo 2
Belezinha, considere dois fatores: e . mostra o total de observações realizadas em no nível do fator de , mostra o total de observações feitas em no nível do fator de , mostra o total de observações na célula , e então correspondendo a linha, coluna, célula e média. Usando as formulas para contruir a tabela :
Para testar se os efeitos do fator de linha são todos iguais a zero (), usando a razão , que tem uma distribuição com e graus de liberdade.
Para testar se os efeitos do fator de coluna são todos iguais a zero (), use a razão , que tem uma distribuição com e graus de liberdade.
Para testar se todos os efeitos de interação são zero, usando a razão com uma distribuição e e graus de liberdade.
Geralmente é melhor realizar o teste para a interação primeiro e depois avaliar os principais efeitos. Se a interação não for significativa, a interpretação do teste sobre os efeitos é simples. Se a interação for significativa, os principais defeitos envolvidos da interação podem não ter muito valor interpretativo prático.
Passo 3
Então, agora fazemos o ANOVA pelo Minitab, e temos como resultado:
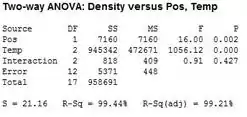
Como o vaor do teste para interação é e é superior a , concluímos que no nível de a interação não é significativa. Portantom podemos continuar testando a hipótese para os principais efeitos.
Uma vez que o valor do teste para isolamento é é inferior a , nós rejeitamos e concluímos que há efeito do isolamento. Uma vez que o valor do teste para a temperatura é que é maior que , não podemos rejeitar e concluímos que não há evidências para o efeito da temperatura. Valor traçar o gráfico de interação para pela temperatura em diferentes níveis de isolamento, o gráfico fica:
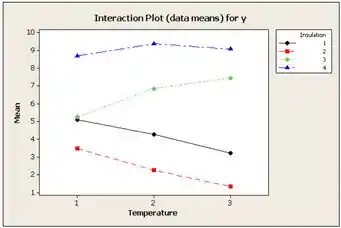
As linhas do gráfico não se cruzam, na verdade, algumas das linha parecem aproximadamente paralelas. Portanto, concluímos que a interação não é significativa nesse experimento.
Passo 4
Agora, plotamos os gráficos de probabilidade normal e de resíduos pelo Minitab:
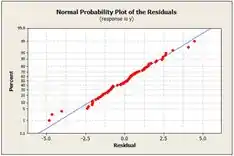
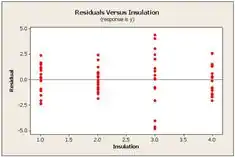
O gráfico de probabilidade normal não indica qualquer partida da normalidade além de alguns pontos na cauda. Os lotes de resíduos são bastante simétricos sobre zero.
Passo 5
Investigando as diferenças entre as densidade médias em três temperaturas diferentes. O estimados de pontos de diferença entre e significa para o fator (tipo de isolamento) é . A variância deste estimador (assumindo que os erros são normalmente distribuídos) é:
Usaremos para estimar . As estatísticas tem uma distribuição com graus de liberdade. Assim, considera-se que a diferença é significativa se for maior que a diferença menos significativa.
Encontrando a densidade média para cada temperatura. Os resultados ficam:

Encontrando o valor do para . Nós temos , , e .
Passo 6
Por fim, encontramos os valores absolutos das diferenças de meios para diferentes temperaturas e comparamos com o valor do . Os resultados ficam:
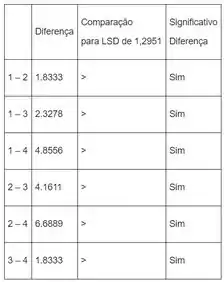
Assim, há uma diferença significativa entre os meios para todos os tipos de isolamento.
Resposta
E:
A interação não é significativa nesse experimento.
Há uma diferença significativa entre os meios para todos os tipos de isolamento.