O artigo “Can We Really Walk Straight?” (Amer. J. of Physical Anthropology, 1992, p. 19-27) relatou um experimento em que cada um de 20 homens saudáveis foi solicitado a caminhar da forma mais reta possível até um alvo a 60m de distância com velocidade normal. Considere as observações a seguir sobre a cadência (número de passos por segundo): 0,95 0,85 0,92 0,95 0,93 0,86 1,00 0,92 0,85 0,81 0,78 0,93 0,93 1,05 0,93 1,06 1,06 0,96 0,81 0,96 Use os métodos desenvolvidos neste capítulo para resumir os dados e inclua interpretações ou discussões, se apropriado. (Nota: O autor do artigo usou uma análise estatística sofisticada para concluir que as pessoas não podem andar em linha reta e sugeriu diversas explicações para isso.

1º A média simples de um valor, dada por:

‎A Média para a Amostra, que tem ‎n=20‎ observações é‎

2º Mediana

A mediana amostral x é obtida a partir de observações ordenadas do menor para o maior, onde incluímos os valores repetidos. Então, a mediana amostral é

Para a amostra temos que n = 20, o número de observações. Como n = 20 é um número par, precisamos encontrar os seguintes valores ordenados

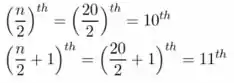
3ª Variância

Onde

4º O desvio padrão da amostra

‎Finalmente, a variância da amostra é‎

‎E o desvio padrão da amostra é‎

5º; 6º; 7º

Suponha que temos n observações. Ordenando a observação do menor para o maior e dividindo as duas metades (metade menor/metade maior, se n for ímpar a mediana está incluído em ambas as metades) definimos o quarto inferior como a mediana da metade menor e o quarto superior como a mediana da metade maior. Quarta página é definido como

Nesta amostra, desde n=20n=20 é um número igual, nós apenas separamos em duas classes com 10 observações. Portanto, a menor metade dos dados é:

0.78, 0.81, 0.81, 0.85, 0.92, 0.92, 0.93, 0.93.

Agora, para a menor metade que temos n=10 observações, que é um número uniforme. Precisamos encontrar os seguintes valores ordenados

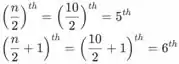
onde o  e  os valores são marcados como vermelhos nos dados menores ordenados da Amostra. Portanto o quarto inferior para os dados da Amostra é

A maior metade dos dados é:

0.93, 0.93, 0.95, 0.95, 0.96, 0.96, 1, 1.05, 1.06, 1.06.

Agora, para a maior metade que temos n=20 observações, que é um número uniforme. Precisamos encontrar os seguintes valores ordenados

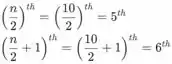
onde o  e os valores são marcados como vermelhos nos dados maiores ordenados da Amostra. Portanto o quarto superior para os dados da Amostra é

O quarto para os dados da amostra é

8º

Observações que estão mais longe do que ​ do quarto mais próximo (superior/inferior) é um Outlier. Se o outlier é mais longe do que ​ a partir do quarto mais próximo dizemos que é um extremo outlier, caso contrário, é Moderada Outlier.

Desde é

Temos que

Usando isso, podemos calcular os limites para os outliers leves e extremos

Os valores discrepantes são todos valores entre 0.540 e 0.6975 bem como entre 1.1175 e 1.275.

Os outliers extremos são todos os valores menores que 0,540,54 e maiores que 1,2751,275.

Não há não existem valores atípicos extremos, pois não há valores menores que 0.540 e maiores que 1,275. Há um outlier moderado, pois não há valores entre 0.540 e 0.6975 bem como entre 1.1175 e 1.2751

BoxPlot:

Agora temos tudo para criar um BoxPlot. As linhas na parte superior e inferior do boxplot são os valores menores/maiores, a linha no boxplot representa a mediana, x marca a média da amostra e a caixa começa no quarto inferior e termina no quarto superior.

A partir do BoxPlot, podemos notar que os dados são assimétricos negativamente (a mediana s no topo da caixa, bem como a média). Conforme calculamos, o desvio padrão é 0.0809 e o quarto spread é 0,1 o que indica que a variação na amostra é pequena. Não há outliers nos dados (veja a miniseção "oitavo").