Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios Suplementares - Ex. 84
O artigo “Evaluating the BOD POD for Assessing Body Fat in Collegiate Football Players” (Medicine and Science in Sports and Exercise, 1999, p. 1350–1356) relata um novo dispositivo de deslocamento de ar para medir a gordura do corpo. O procedimento habitual utiliza o dispositivo de pesagem hidrostática, que mede a porcentagem de gordura do corpo por meio do deslocamento de água. Aqui são apresentados dados representativos reproduzidos de um gráfico desse artigo.
Passo 1
- Um método para decidir o necessário é o teste t pareado.
- O gráfico sugere que um modelo de regressão linear simples ajusta os dados; assim, estime os parâmetros usando o método dos mínimos quadrados
Quando (diferença entre observações dentro de um par), e hipótese nula
o valor da estatística de teste para testar as hipóteses é
onde e são a média amostral e o desvio padrão amostral das diferenças , respectivamente. Para usar este teste, suponha que as diferenças são de uma população normal. Dependendo da hipótese alternativa, o valor de P pode ser determinado como a área correspondente sob o curva.
As hipóteses de interesse são versus . A tabela a seguir representa os dados para BOD e HW, bem como a diferença entre os pares observados correspondentes:
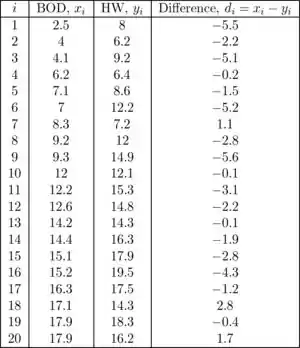
Passo 2
A média amostral para as diferenças é
O único valor ausente para calcular o valor estatístico do teste é o desvio padrão da amostra das diferenças
A variância da amostra s² é
Onde
O desvio padrão da amostra s é
A variância da amostra é
e o desvio padrão da amostra
O valor da estatística de teste é
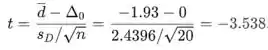
O teste é bilateral onde a hipótese alternativa é , portanto, o valor de P é a área sob o curva à direita do valor |t| vezes dois
onde T tem distribuição de estudantes com 19 graus de liberdade, e a probabilidade calculada usando software (você pode usar a tabela no apêndice do livro). No nível de significância 0.01, porque
rejeitar hipótese nula em determinado nível de significância e concluir que as leituras médias verdadeiras para os dois métodos são diferentes.
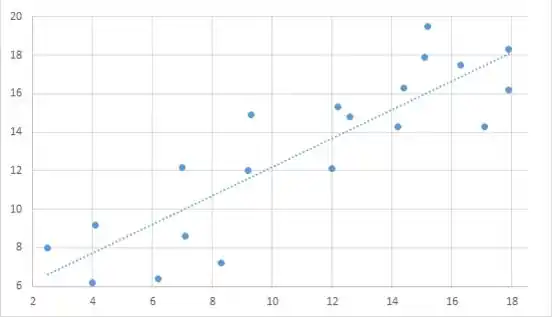
A estimativa de mínimos quadrados da inclinação no modelo de regressão linear simples é
A estimativa de mínimos quadrados da intersecção é
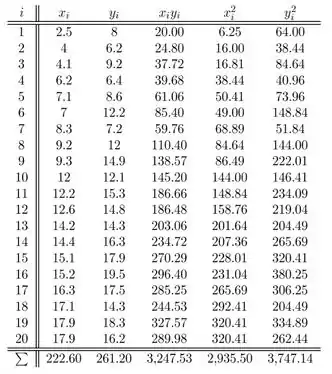
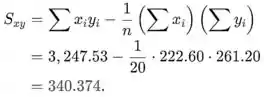
Encontrando e usando as somas dadas no exercício, a estimativa do intercepto é
Passo 2
Nós estamos testando contra uma das alternativas,
Dependendo da hipótese alternativa, o valor P pode ser determinado como área correspondente sob . O teste de utilidade do modelo:
A variância e o desvio padrão do estimador são
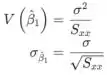
Onde
Ao estimar o desvio padrão σ com s você obtém estimativa de
A soma dos quadrados dos erros, SSE, é
A estimativa do desvio padrão é
A soma dos quadrados dos erros, SSE, é
A fórmula computacional para SSE é
O valor de P é a área correspondente sob a curva
que foi calculado por meio de um software. Finalmente, desde
rejeitar hipótese nula em determinado nível de significância ou qualquer nível de significância razoável. Existe uma relação significativa entre as duas variáveis.
O coeficiente de correlação da amostra r é dado por
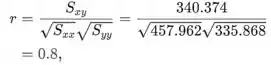
A relação entre o coeficiente de correlação da amostra e o coeficiente de determinação é dada por
assim, o coeficiente de determinação, ou a proporção de variação observada é
Isso indica que 75% da variação observada em y é atribuída à regressão linear, que não é muito - é moderada.
Resposta
- Rejeite a hipótese nula, as médias verdadeiras diferem;
- Use o método dos mínimos quadrados para estimar os parâmetros e analisar para confirmar a eficácia.