Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios Suplementares - Ex. 85

Reconsidere a situação do Exercício 68, no qual x = % de entrada térmica de RDF e y = % de eficiência de uma determinada caldeira foram relacionadas por meio de um modelo de regressão linear simples. Suponha que, para uma segunda caldeira, essas variáveis sejam também relacionadas por meio do modelo de regressão linear simples e que para ambas as caldeiras. Se o conjunto de dados consistir em n1 observações para a primeira caldeira e n2 para a segunda e se SQE1 e SQE2 representarem as duas somas de quadrados do erro, então uma estimativa conjunta de 2 e ˆ2 (SQE1 SQE2)/ (n1 n2 – 4). Representemos SSx1 e SSx2 por (xi x )2 para os dados na primeira e na segunda caldeiras, respectivamente. Um teste de H0: 1 1 0 (coeficientes angulares iguais) baseia-se na estatística

Quando H0 é verdadeira, T tem uma distribuição t com n1 n2 4 gl. Suponha que as seis observações sobre a segunda caldeira sejam (0, 81,3), (10, 78,4), (20, 78,2), (25, 79,1), (30, 77,6) e (40, 77,4). Usando esses valores com os dados do Exercício 68, realize um teste no nível 0,05 para verificar se a mudança esperada na % de eficiência associada com um aumento de 1% na entrada térmica de RDF é idêntica para as duas caldeira

Passo 1

Usando a saída do SAS do exercício mencionado, os dados a seguir são necessários para testar as hipóteses apropriadas

Erro de soma dos quadrados , pode ser calculado como

Primeira estimativa de cálculo de σ²da fórmula dada como

Passo 2

Valor da estatística de teste quando a hipótese nula é é

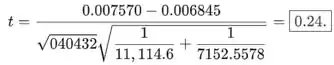
A hipótese alternativa é , que é bicaudal; assim, usando um software o valor de P é

não rejeite a hipótese nula em qualquer nível de significância razoável α. É plausível supor que

Resposta

É plausível supor que

Exercícios de Livros Relacionados

Usamos uma amostra de 30 observações para ajustar um modelo de regressão. O modelo completo tem nove regressores, sendo a variância estimada σ 2 = M Q L = 100eR 2 = 0.92 .a)Calcule a estatística F par

Mostre que podemos expressar os resíduos de um modelo de regerssão múltipla como e = 1 - H y , sendo H = X X ' X - X .

Mostre que a variância do i-ésimo resíduo e, em um modelo de regressão múltipla é σ 2 ( 1 - h H ) e que a covariância entre e i e e j é -sigmah, sendo os h’s os elementos da mesma regressão do item pa

Considere os dados sobre a impulsão do motor no exercício 12-88. Reajuste o modelo usando y * = ln ⁡ y como a variável de resposta e x 3 * = ln ⁡ x 3 como o regressor (juntamente com x 4 e x 5 ).(a)Te

Uma amostra de 25 observações é usada para ajustar um modelo de regressão com sete varíaveis. A estimativa de σ 2 para esse modelo completo é M Q E = 10 .a)Um algoritimo de seleção progressiva colocou